
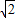 ≈1.41,
≈1.41,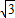 ≈1.73)
≈1.73)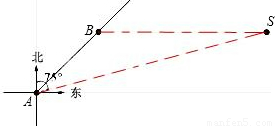
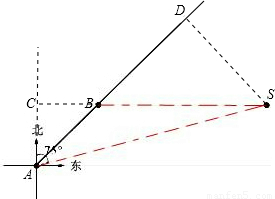 解:作与正北方向平行的直线,与SB的延长线相交于点C,过点S作SD⊥AB于D.
解:作与正北方向平行的直线,与SB的延长线相交于点C,过点S作SD⊥AB于D. =6(海里),
=6(海里),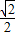 =3
=3 (海里),
(海里),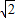 ×(2+
×(2+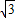 )=6
)=6 +3
+3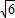 (海里),
(海里),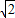 +3
+3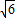 (海里),
(海里),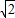 +3
+3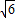 )×
)×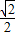 =3+3
=3+3 ≈8.2>8,
≈8.2>8,

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
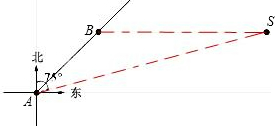 船可以继续沿东北方向航行吗?为什么?(参考数据:
船可以继续沿东北方向航行吗?为什么?(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
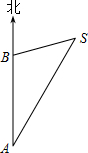 如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)
如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
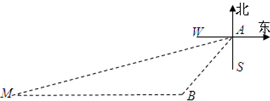 如图,一艘船以每小时40海里的速度向西南方向航行,在A处观测灯塔M在船的南偏西75°的方向,航行9分钟后到达B处,这时灯塔M恰好在船的正西方向.已知距离此灯塔9海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:
如图,一艘船以每小时40海里的速度向西南方向航行,在A处观测灯塔M在船的南偏西75°的方向,航行9分钟后到达B处,这时灯塔M恰好在船的正西方向.已知距离此灯塔9海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市进化一中中考数学模拟试卷 题型:解答题
(2011四川泸州,25,7分)如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)
(1)求船在B处时与灯塔S的距离;
(2)若船从B处继续向正北方向航行,问经过多长时间船与灯塔S的距离最近.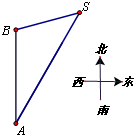
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com