
 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°:分析 (1)①根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;②根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;
(2)根据∠ACE=90°-∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论;
(3)分五种情况进行讨论:当CB∥AD时,当EB∥AC时,当CE∥AD时,当EB∥CD时,当BE∥AD时,分别求得∠ACE角度.
解答  (1)①∵∠DCE=45°,∠ACD=90°
(1)①∵∠DCE=45°,∠ACD=90°
∴∠ACE=45°
∵∠BCE=90°
∴∠ACB=90°+45°=135°
故答案为:135°;
②∵∠ACB=140°,∠ECB=90°
∴∠ACE=140°-90°=50°
∴∠DCE=90°-∠ACE=90°-50°=40°;
(2)猜想:∠ACB+∠DCE=180°
理由如下:∵∠ACE=90°-∠DCE
又∵∠ACB=∠ACE+90°
∴∠ACB=90°-∠DCE+90°=180°-∠DCE
即∠ACB+∠DCE=180°;
(3)15°、30°、45°、120°、135°、165°.
理由:当CB∥AD时,∠ACE=30°;
当EB∥AC时,∠ACE=45°;
当CE∥AD时,∠ACE=120°;
当EB∥CD时,∠ACE=135°;
当BE∥AD时,∠ACE=165°或15°.
点评 本题主要考查了平行线的性质,以及直角三角形的性质,解题时注意分类讨论思想的运用,分类时注意不能重复,也不能遗漏.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
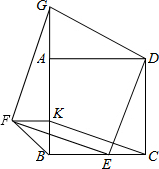 如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.
如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将两块大小相同的直角三角尺(即三角形ABC和三角形DEF,其中∠A=∠D=30°,按如图所示的方式摆放(直角顶点F在斜边AB上,直角顶点C在斜边DE上),且DE∥AB.
将两块大小相同的直角三角尺(即三角形ABC和三角形DEF,其中∠A=∠D=30°,按如图所示的方式摆放(直角顶点F在斜边AB上,直角顶点C在斜边DE上),且DE∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com