
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB。

(1)△BPQ是 三角形;
(2)求PQ的长度;
(3)求∠APB的度数。
【答案】(1)等边;(2)PQ=4;(3)∠APB=150°
【解析】
(1)连接PQ,由旋转的性质可得△BAP≌△BCQ,可推出BP=BQ,∠PBQ=60°,进而得到等边△BPQ;
(2)△BPQ为等边三角形,所以PQ=PB=4;
(3)由PQ=4,CQ=3,PC=5,可得出△PCQ为直角三角形,∠PQC=90°,由∠APB=∠CQB可得结果.
(1)连接PQ,
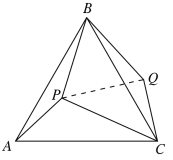
由旋转的性质可得△BAP≌△BCQ,
∴∠ABP=∠CBQ,BP=BQ,
又∵∠ABC=60°,
∴∠ABP+∠PBC=60°
∴∠CBQ+∠PBC=60°,即∠PBQ=60°,
∴△BPQ为等边三角形,
(2)∵△BPQ为等边三角形,
∴PQ=PB=4
(3)∵△BAP≌△BCQ,
∴CQ=PA=3,
在△PCQ中,PQ=4,CQ=3,PC=5,
∵32+42=52,即CQ2+PQ2=PC2,
∴△PCQ为直角三角形,∠PQC=90°,
又∵△BPQ为等边三角形,
∴∠BQP=60°,
∴∠CQB=∠BQP+∠PQC=150°
∵△BAP≌△BCQ,
∴∠APB=∠CQB=150°.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)若该抛物线的顶点是点D,求四边形OCDB的面积;
(3)已知点P是该抛物线对称轴的一点,若以点P,O,D为顶点的三角形是等腰三角形,请直接写出点P的坐标.(不用说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
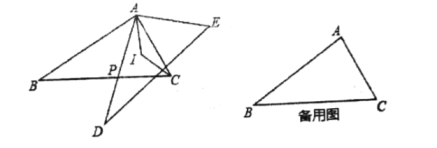
【题目】如图,△ABC和△ADE中,![]() ,
,![]() ,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,AI、CI分别平分
,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,AI、CI分别平分![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,请用含
,请用含![]() 的式子表示PD,并求PD的最大值;
的式子表示PD,并求PD的最大值;
(3)当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,分别直接写出m,n的值.
,分别直接写出m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_______cm/s时,能够使△BPE≌△CQP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为
米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为![]() 米,一级台阶高为
米,一级台阶高为![]() 米,如图所示,若此时落在地面上的影长为
米,如图所示,若此时落在地面上的影长为![]() 米,则树高为( )
米,则树高为( )

A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() ,
,![]() ,则对于下列结论:
,则对于下列结论:
①当![]() 时,
时,![]() ;
;
②方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ;
;
③![]() .
.
其中正确的结论有________(只需填写序号即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com