
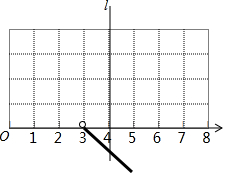
 如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.
如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹. 科目:初中数学 来源: 题型:解答题
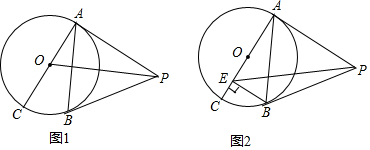 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
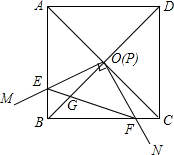 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com