
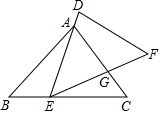
 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AD}{AE}$=$\frac{GF}{GE}$ | C. | $\frac{AG}{AC}$=$\frac{EG}{EF}$ | D. | $\frac{ED}{EF}$=$\frac{EG}{EA}$ |
分析 利用两组对应边的比相等且夹角对应相等的两个三角形相似可由$\frac{AB}{BC}$=$\frac{DE}{EF}$得到△ABC∽△EDF;利用$\frac{AD}{AE}$=$\frac{GF}{GE}$或$\frac{ED}{EF}$=$\frac{EG}{EA}$可根据两组对应边的比相等且夹角对应相等的两个三角形相似先判断△DEF∽△AEG,再利用有两组角对应相等的两个三角形相似判定△AEG∽△ABC,从而得到△ABC∽△EDF,于是可对各选项进行判断.
解答 解:当$\frac{AB}{BC}$=$\frac{DE}{EF}$时,则$\frac{AB}{DE}$=$\frac{BC}{EF}$,而∠B=∠AEG,所以△ABC∽△EDF;
当$\frac{AD}{AE}$=$\frac{GF}{GE}$,则$\frac{DE}{AE}$=$\frac{EF}{EG}$,而∠DEF=∠AEG,所以△DEF∽△AEG,又因为AE=EC,所以∠EAG=∠C,而∠AEG=∠B,所以△AEG∽△ABC,所以△ABC∽△EDF;
当$\frac{ED}{EF}$=$\frac{EG}{EA}$,则$\frac{DE}{AE}$=$\frac{EF}{EG}$,而∠DEF=∠AEG,所以△DEF∽△AEG,又因为AE=EC,所以∠EAG=∠C,而∠AEG=∠B,所以△AEG∽△ABC,所以△ABC∽△EDF.
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.


科目:初中数学 来源: 题型:填空题
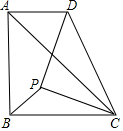 如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为$\sqrt{2}$.
如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O是原点,直线y=$\frac{3}{4}$x-3分别交x轴、y轴于点A、点C,点B在y轴正半轴上,且OB=OA.点D(2,m)在直线AB上,点P是x轴上的一个动点,设点P的横坐标为t.
如图,在平面直角坐标系中,O是原点,直线y=$\frac{3}{4}$x-3分别交x轴、y轴于点A、点C,点B在y轴正半轴上,且OB=OA.点D(2,m)在直线AB上,点P是x轴上的一个动点,设点P的横坐标为t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
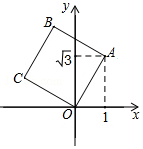 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )| A. | (1-$\sqrt{3}$,$\sqrt{3}$+1) | B. | (-$\sqrt{3}$,$\sqrt{3}$+1) | C. | (-1,$\sqrt{3}$+1) | D. | (-1,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | (x3)2=x5 | C. | x6÷x3=x2 | D. | ($\frac{1}{2}$)-2=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com