练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线AB、CD相交于点O，下列条件中，不能说明AB⊥CD的是(　　)

    A. ∠AOD＝90°

    B. ∠AOC＝∠BOC

    C. ∠BOC＋∠BOD＝180°

    D. ∠AOC＋∠BOD＝180°

    【答案】C

    【解析】

    根据垂直的定义分析即可，两条直线相交所成的4个角中，如果有一个角等于90°，那么这两条直线互相垂直.

    A. ∵ ∠AOD=90° ，∴ AB⊥CD，故正确；

    B. ∵∠AOC=∠BOC，∠AOC+∠BOC=180°，∴∠AOC=∠BOC=90°，∴ AB⊥CD，故正确；

    C. 由∠BOC+∠BOD=180° 不能说明哪一个角是直角，故不正确；

    D. ∵∠AOC+∠BOD=180°，∠AOC=∠BOD，∴∠AOC+∠BOD=90°，∴ AB⊥CD，故正确；

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解决问题：

    一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5千米到达小颖家，然后向西走了10千米到达小明家，最后回到超市．

    （1）以超市为原点，以向东的方向为正方向，用1个单位长度表示1千米，在数轴上表示出小明家，小彬家，小颖家的位置．

    （2）小明家距小彬家多远？

    （3）货车一共行驶了多少千米？

    （4）货车每千米耗油0.2升，这次共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为等腰直角三角形，∠BAC=90°，BC=2，E为AB上任意一动点，以CE为斜边作等腰Rt△CDE，连接AD，下列说法：①∠BCE=∠ACD；②AC⊥ED；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD的面积有最大值，且最大值为 ．其中，正确的结论是（ ）
    A.①②④
    B.①③⑤
    C.②③④
    D.①④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

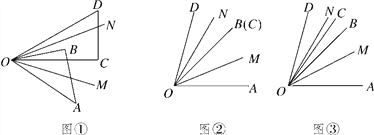
    【题目】如图①，将一副三角板的两个锐角顶点放到一块，∠AOB＝45°，∠COD＝30°，OM，ON分别是∠AOC，∠BOD的平分线．

    (1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②)，则∠MON的大小为________；

    (2)如图③，在(1)的条件下，继续绕着点O逆时针旋转∠COD，当∠BOC＝10°时，求∠MON的大小，写出解答过程；

    (3)在∠COD绕点O逆时针旋转过程中，∠MON＝________°.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂现有甲种原料226 kg，乙种原料250 kg，计划利用这两种原料生产A、B两种的产品共40件，生产A、B两种产品用料情况如下表：

    若设生产A产品件，求的值，并说明有哪几种符合题意的生产方案。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2015秒时，点P的坐标是（ ）

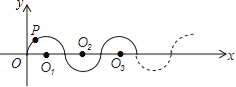
    A. （2014，0） B. （2015，﹣1） C. （2015，1） D. （2016，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点A，B，C，D分别表示－3，－1，0，4.请解答下列问题：

    (1)在数轴上描出A，B，C，D四个点；

    (2)现在把数轴的原点取在点B处，其余均不变，那么点A，B，C，D分别表示什么数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线a，b相交．

    (1)已知∠1＝40°，求∠2，∠3，∠4；

    (2)已知∠2＋∠4＝280°，求各角；

    (3)已知∠1∶∠2＝2∶7，求各角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y＝(k为常数)．

    (1)k为何值时，该函数是正比例函数；

    (2)k为何值时，正比例函数过第一、三象限，写出正比例函数解析式；

    (3)k为何值时，正比例函数y随x的增大而减小，写出正比例函数的解析式．

    查看答案和解析>>

    同步练习册答案