
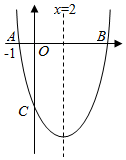
 如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0)
如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0)分析 (1)利用待定系数法求抛物线的解析式;
(2)由对称性可直接得出B(5,0),当x=0时,代入抛物线的解析式可得与y轴交点C的坐标;
(3)根据90°所对的弦是直径可知:过O,B,C三点的圆的直径是线段BC,利用勾股定理求BC的长,代入圆的面积公式可以求得面积.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{-\frac{b}{2}=2}\\{1-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=-5}\end{array}\right.$,
∴抛物线的解析式为:y=x2-4x-5;
(2)∵对称轴为直线x=2,A(-1,0),
∴B(5,0),
当x=0时,y=-5,
∴C(0,-5),
(3)∵∠BOC=90°,
∴BC是过O,B,C三点的圆的直径,
由题意得:OB=5,OC=5,
由勾股定理得;BC=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
S=π•$(\frac{5\sqrt{2}}{2})^{2}$=$\frac{25}{2}$π,
答:过O,B,C三点的圆的面积为$\frac{25}{2}$π.
点评 本题考查了利用待定系数法求抛物线的解析式和抛物线与两坐标轴的交点,明确令x=0时,求抛物线与y轴的交点;令y=0时,求抛物线与x轴的交点;同时要想求过O,B,C三点的圆的面积就要先求圆的半径可直径,根据圆周角定理可以解决这个问题,从而使问题得以解决.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
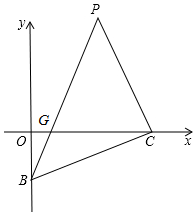 如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.
如图,点D(m,n)满足m2-6m+$\sqrt{m+n-6}$=-9,B为y轴负半轴上一动点,∠DBC=45°,BC交x轴于C,CP⊥BC交BD延长线于P,交x轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,如图所示,在不添加任何辅助线的情况下:若DB平分∠ADC,请找出图中与△ABE相似的所有三角形,并选择其中一对进行证明.
梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,如图所示,在不添加任何辅助线的情况下:若DB平分∠ADC,请找出图中与△ABE相似的所有三角形,并选择其中一对进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a,b同号,且两数相差1 | |
| B. | a,b异号,且负数的绝对值比正数大1 | |
| C. | a,b同号,且两数和为1 | |
| D. | a,b异号,且正数比负数的绝对值大1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com