
 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程cx2+bx-a=0是关于x的一元二次方程.
已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程cx2+bx-a=0是关于x的一元二次方程.分析 (1)先计算判别式的值得到△=b2+4a•c,由于a、b、c为三角形的边长,则△>0,然后根据判别式的意义判断方程根的情况;
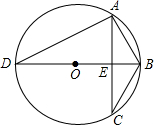
(2)连接OA,如图,根据垂径定理,由BD⊥AC得到,弧AB=弧CB,弧AD=弧CD,再利用圆心角、弧、弦的关系得到AB=CB,利用圆周角定理得到∠ABD=∠DAC=60°,则可判断△OAB为等边三角形,得到AB=OB=2,AE=$\frac{\sqrt{3}}{2}$OB=$\sqrt{3}$,所以AC=2AE=2$\sqrt{3}$,即a=2,b=2$\sqrt{3}$,c=2,然后利用求根公式法解方程2x2+2$\sqrt{3}$x-2=0;
(3)根据一元二次方程根的定义,把x=$\frac{1}{4}$a代入cx2+bx-a=0后变形得到$\frac{ac}{4}$=4-b,易得b<4,利用a、b、c的长均为整数得到b=1,2,3,然后分类讨论:当b=1时,ac=12,;当b=2时,ac=8;当b=3时,ac=4,再利用整数的整除性求出a、c的值,然后利用三角形三边的关系确定满足条件的a、b、c的值.
解答 解:(1)△=b2-4a•(-c)=b2+4a•c,
∵a、b、c分别为∠A、∠B、∠C的对边,即a、b、c都是正数,
∴△>0,
∴方程有两个不相等的实数根;
故答案为:②;
(2) 连接OA,如图,
连接OA,如图,
∵BD⊥AC,∠D=30°,
∴弧AB=弧CB,弧AD=弧CD,∠DAC=60°,
∴AB=CB,∠ABD=∠DAC=60°,
∴△OAB为等边三角形,
∴AB=OB=2,
∴AE=$\frac{\sqrt{3}}{2}$OB=$\sqrt{3}$,
∴AC=2AE=2$\sqrt{3}$,
即a=2,b=2$\sqrt{3}$,c=2,
方程cx2+bx-a=0变形为2x2+2$\sqrt{3}$x-2=0,
整理得方${x}^{2}+\sqrt{3}x$-1=0,
解得:${x}_{1}=\frac{-\sqrt{3}-\sqrt{7}}{2}$,${x}_{2}=\frac{-\sqrt{3}+\sqrt{7}}{2}$.
(3)把x=$\frac{1}{4}$a代入cx2+bx-a=0得$c•\frac{1}{16}{a}^{2}+b•\frac{1}{4}a-a$=0,
整理得$\frac{ac}{4}$=4-b,则4-b>0,
即b<4,
∵a、b、c的长均为整数,
∴b=1,2,3,
当b=1时,ac=12,则a=1,c=12;a=2,c=6;a=3,c=4;a=6,c=2;a=12,c=1,都不符合三角形三边的关系,舍去;
当b=2时,ac=8,则a=1,c=8;a=2,c=4;a=4,c=2;a=8,c=1,都不符合三角形三边的关系,舍去;
当b=3时,ac=4,则a=1,c=4;a=2,c=2;a=4,c=1,其中a=2,c=2符合三角形三边的关系,
∴a=2,b=3,c=2.
点评 本题考查了圆的综合题:熟练掌握垂径定、圆周角定理和等边三角形的判定与性质;会运用根的判别式判断一元二次方程根的情况和解一元二次方程;理解一元二次方程解的意义和三角形三边的关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
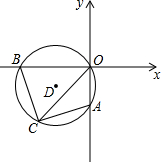 如图,在平面直角坐标系中,过原点的⊙D交坐标轴于A、B两点,且A(0,-2),OC平分∠AOB且交⊙D于点C,AC+BC=2$\sqrt{10}$.
如图,在平面直角坐标系中,过原点的⊙D交坐标轴于A、B两点,且A(0,-2),OC平分∠AOB且交⊙D于点C,AC+BC=2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com