练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

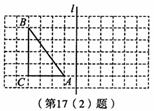
    如图，在边长为1个单位长度的小正方形所组成的网格中，△ABC的顶点均在格点上.

         ①sinB的值是             ；

         ②画出△ABC关于直线l对称的△A1B1C1（A与A1，B与B1，C与C1相对应）.连接AA1，BB1，并计算梯形AA1B1B的面积.


    ①；

       ②如图所示.

       由轴对称的性质可得，AA1=2，BB1=8，高是4.

       ∴ =(AA1+BB1)´4=20.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     (1) 已知线段AB在平面内,在平面内找一点P使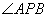=90°

         (2) 请反思这样的P点有几个，共同特征是什么.

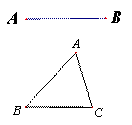
    (3) 做如图三角形AB边上的高线（不能用含90°的直角三角尺）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    定义新运算“”，规则：，如，。若的两根为，则＝                ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若(m-1)2+      =0，则m+n的值是

       A．-1              B．0              C．1               D．2     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在□ABCD中，DE平分∠ADC，AD=6，BE=2，则□ABCD的周长是       .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


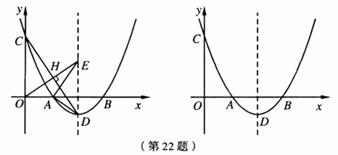
    如图，抛物线y=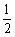(x-3)2-1与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D了.

    （1）求点A，B，D的坐标；

    （2）连接CD，过原点O作OE⊥CD，垂足为H，OE与抛物线的对称轴交于点E，连接AE，AD.求证：∠AEO=∠ADC；

    （3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙E的切线，切点为Q，当PQ的长最小时，求点P的坐标，并直接写出点Q的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若点M(x，y)满足(x+y)2 =x2 +y2 -2，则点M所在象限是

      A．第一象限或第三象限    B．第二象限或第四象限

      C．第一象限或第二象限    D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


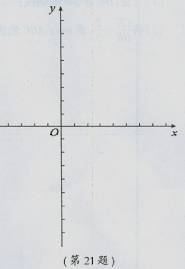
    在平面直角坐标系xOy，已知抛物线y=x2-2mx+m2-9．

    (1)求证：无论m为何值，该抛物线与x轴总有两个交点；

    (2)该抛物线与x轴交于A，B两点，点A在点B的左侧，且OA＜OB，与y轴的交点坐标为（O，-5），求此抛物线的解析式；

    (3)在(2)的条件下，抛物线的对称轴与x轴的交点为N，若点M是线段AN上的任意一点，过点M作直线MC⊥x轴，交抛物线于点C，记点C关于抛物线对称轴的对称点为D，点P是线段MC上一点，且满足MP=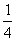MC，连结CD,PD，作PE⊥PD交x轴与点E,问是否存在这样的点E，使得PE=PD，若存在，求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为点G.

    求证：AE=BF.

     


    查看答案和解析>>

    同步练习册答案