
分析 (1)由已知等式知,连续奇数乘积的倒数等于各自倒数差的一半,据此可得;
(2)根据以上规律可得原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$),即可得出答案.
解答 解:(1)由已知等式知,连续奇数乘积的倒数等于各自倒数差的一半,
∴第n个等式为$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);
(2)原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{201}$)
=$\frac{1}{2}$×$\frac{200}{201}$
=$\frac{100}{201}$.
点评 本题主要考查数字的变化规律,根据题意得出连续奇数乘积的倒数等于各自倒数差的一半且掌握裂项求和是解题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
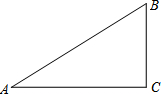 已知:如图,在△ABC中,∠A=30°,∠B=60°.
已知:如图,在△ABC中,∠A=30°,∠B=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com