
【题目】如图,以扇形 OAB 的顶点 O 为原点,半径 OB 所在的直线为 x 轴,建立平面直角坐标系,点 B 的坐标为(2,0),若抛物线 ![]() (n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )
(n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )

A.n>-4B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】2018年1月19日,中欧(厦门-西安-布达佩斯)班列驶出厦门自贸区海沧火车站,经西安直达匈牙利首都布达佩斯 ,我市与欧洲各国经贸往来日益频繁,某欧洲客商准备在厦门采购一批特色商品,经调查,用![]() 元采购
元采购![]() 型商品的件数是用
型商品的件数是用![]() 元采购
元采购![]() 型商品件数的
型商品件数的![]() 倍,一件
倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多
型商品的进价多![]() 元.
元.
(1)求一件![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该欧洲客商购进![]() 型商品共
型商品共![]() 件进行试销,其中
件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型商品的件数,且不小于
型商品的件数,且不小于![]() 件,已知
件,已知![]() 型商品的售价为
型商品的售价为![]() 元/件,
元/件,![]() 型商品的售价为
型商品的售价为![]() 元/件,且全部售出,设购进
元/件,且全部售出,设购进![]() 型商品
型商品![]() 件.
件.
①求该客商销售这批商品的利润![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
②若欧洲商决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,求该客商售完所有商品并捐献资金后获得的最大收益.
元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
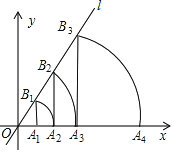
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
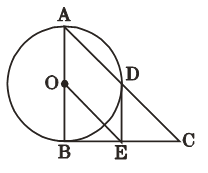
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:![]()
(3)若tanC=![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地有一个直径为 14 米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心 2 米处达到最高,高度为5米 ,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示以水平方向为 x 轴,喷水池中心为原点建立直角坐标系.
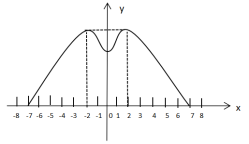
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高 1.8 米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估规划,政府决定对喷水设施改造成标志性建筑,做出如下设计改进;在喷出水柱的形状不变的前提下,把水池的直径扩大到 42 米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
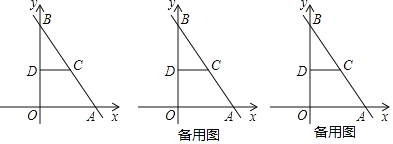
(1)求点D的坐标;
(2)点P从点O出发,以每秒1个单位长度的速度沿OA匀速运动,同时点Q从点A出发,以每秒![]() 个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
(3)在(2)的条件下,过点Q作RQ⊥AB交y轴于点R,连接AD,点E为AD中点,连接OE,求t为何值时,直线PR与x轴相交所成的锐角与∠OED互余.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得![]() ,即
,即![]() ;由周长为m,得
;由周长为m,得![]() ,即
,即![]() .满足要求的
.满足要求的![]() 应是两个函数图象在第 象限内交点的坐标.
应是两个函数图象在第 象限内交点的坐标.
(2)画出函数图象
函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象可由直线
的图象可由直线![]() 平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线![]() .
.
(3)平移直线![]() ,观察函数图象
,观察函数图象
①当直线平移到与函数![]() 的图象有唯一交点
的图象有唯一交点![]() 时,周长m的值为 ;
时,周长m的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com