
【题目】如图,AB是![]() 的直径,C是半圆AB上一点,连AC、OC,AD平分
的直径,C是半圆AB上一点,连AC、OC,AD平分![]() ,交弧BC于D,交OC于E,连OD,CD,下列结论:
,交弧BC于D,交OC于E,连OD,CD,下列结论:
①弧![]() 弧CD;②
弧CD;②![]() ;③
;③![]() ;④当C是半圆
;④当C是半圆![]() 的中点时,则
的中点时,则![]() .其中正确的结论是( )
.其中正确的结论是( )
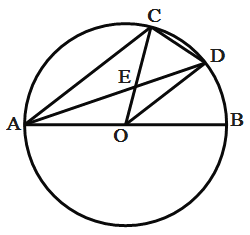
A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
根据圆周角定理得出弧CD=弧BD,推出CD=BD,求出∠DOB=2∠DAB,∠CAB=2∠DAB,根据平行线判定推出AC∥OD,根据三角形外角性质即可判断③,连接BD、BE,求出BD=DE,求出BD=CD,即可得出答案.
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴弧BD=弧CD,∴①正确;
∵OA=OD,
∴∠ODA=∠OAD,
∴∠BOD=∠ODA+∠OAD=2∠DAB,
∵AD平分∠CAB,
∴∠CAB=2∠DAB,
∴∠DOB=∠CAB,
∴AC∥OD,∴②正确;
∵∠ACD=∠ACO+∠OCD,∠OED=∠OCD+∠CDA,
根据已知不能推出∠ACO=∠CDA,∴∠ACD=∠OED不对,∴③错误;
连接BD,BE,
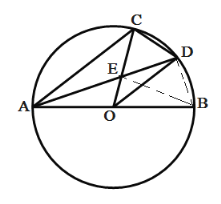
∵C为弧AB中点,
∴∠CAB=45°,
∴∠DAB=22.5°,
∵AB是直径,
∴∠ADB=90°,
∴∠DBA=67.5°,
∵C为弧AB中点,
∴OC⊥AB,
∵OA=OB,
∴AE=BE,
∴∠EBA=∠DAB=22.5°,
∴∠DBE=67.5°-22.5°=45°,
∴∠DEB=180°-90°-45°=45°=∠DBE,
∴DE=BD,
∵弧CD=弧BD,
∴CD=BD,
∴CD=DE,∴④正确;
故选B.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+8ax(a>0)与x轴交于O,A两点,顶点为M,对称轴与x轴交于H,与过O,A,M三点的⊙Q交于点B,⊙Q的半径为5,点C从点B出发,沿着圆周顺时针向点M运动,射线MC与x轴交于D,与抛物线交于E,过点E作ME的垂线交抛物线的对称轴于点F.
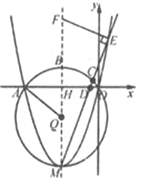
(1)求抛物线的解析式;
(2)当点C的运动路径长为![]() 时,求证:HD=2
时,求证:HD=2![]() HA.
HA.
(3)在点C运动过程中.是否存在这样的位置,使得以点M,E,F为顶点的三角形与△AHQ相似?若存在,求出此位置时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
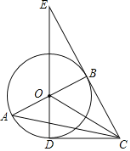
(1) 判断直线CD与⊙O的位置关系,并说明理由;
(2) 若BE=![]() ,DE=3,求⊙O的半径及AC的长.
,DE=3,求⊙O的半径及AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
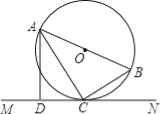
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
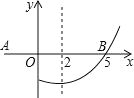
【题目】如图是抛物线 y=ax![]() +bx+c 的一部分,其对称轴为直线 x=2,若其与 x 轴的一个交点为(5,0),则由图象可知,不等式 ax
+bx+c 的一部分,其对称轴为直线 x=2,若其与 x 轴的一个交点为(5,0),则由图象可知,不等式 ax![]() +bx+c<0 的解集是________.
+bx+c<0 的解集是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com