
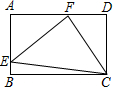
 如图,E、F分别是矩形ABCD的边AB、AD上的点,∠FEC=∠FCE=45°
如图,E、F分别是矩形ABCD的边AB、AD上的点,∠FEC=∠FCE=45°分析 (1)由AAS证明△AEF≌△DFC,即可得出结论;
(2)由△EFC的面积求出EF=CF,由勾股定理求出EC,再由勾股定理求出BE即可.
解答 (1)证明:∵∠FEC=∠FCE=45°,
∴EF=CF,∠CFE=90°,
∴∠AFE+∠DFC=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°.
∴∠AEF+∠AFE=90°.
∴∠AEF=∠DFC.
∴△AEF≌△DFC.
∴AF=CD.
(2)解;∵在Rt△EFC中,${S_{△EFC}}=\frac{1}{2}EF•FC=\frac{1}{2}E{F^2}$,
又∵△EFC的面积为$\frac{3}{2}$,
∴$EF=CF=\sqrt{3}$.
∴$EC=\sqrt{E{F^2}+C{F^2}}=\sqrt{6}$.
∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=2.
∴在Rt△BCE中,$BE=\sqrt{C{E^2}-B{C^2}}=\sqrt{6-4}=\sqrt{2}$.
点评 本题主要考查矩形的性质、全等三角形的判定和性质、勾股定理;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 向左平移4单位 | B. | 向右平移4单位 | C. | 向左平移8单位 | D. | 向右平移8单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
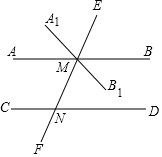 (1)完成下面的证明.
(1)完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.设甲、乙两人间的距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,下列结论中,错误的是( )
甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.设甲、乙两人间的距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,下列结论中,错误的是( )| A. | 出发1小时时,甲、乙在途中相遇 | |
| B. | 出发1.5小时时,乙比甲多行驶了60千米 | |
| C. | 出发3小时时,甲、乙同时到达终点 | |
| D. | 甲的速度是乙速度的一半 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com