
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于点
轴交于点 ![]() 、
、 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() .
.
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() 于
于 ![]() ,
, ![]() 为线段
为线段 ![]()
上一点, ![]() 为
为 ![]() 轴负半轴上一点,以
轴负半轴上一点,以 ![]() 、
、 ![]() 、
、 ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似;
相似;
满足条件的 ![]() 点有且只有一个时,求
点有且只有一个时,求 ![]() 的取值范围;
的取值范围;
②若满足条件的 ![]() 点有且只有两个,直接写出
点有且只有两个,直接写出 ![]() 的值.
的值.
【答案】
(1)解:设抛物线的解析式为y=a(x+1)(x-3),将C(0,3)代入得:3=-3a,解得a=-1,∴抛物线的解析式为y=-x2+2x+3
(2)解:∵x=- ![]() =1,∴CE=1.将x=0代入抛物线的解析式得:y=3,∴点C(0,3).∴ED=3.设EP=x,则(0<x<3).当△CEP∽△QDP时,则
=1,∴CE=1.将x=0代入抛物线的解析式得:y=3,∴点C(0,3).∴ED=3.设EP=x,则(0<x<3).当△CEP∽△QDP时,则 ![]() ,即
,即 ![]() ,
,
整理得:m=2- ![]() ,∴m随x的增大而增大,∴m<1.∵Q在x轴的负半轴上,∴m<0.当△CEP∽△PDQ时,
,∴m随x的增大而增大,∴m<1.∵Q在x轴的负半轴上,∴m<0.当△CEP∽△PDQ时, ![]() ,即
,即 ![]() ,整理得:m=x2-3x+1,∴当x=
,整理得:m=x2-3x+1,∴当x= ![]() 时,m有最小值,m的最小值=-
时,m有最小值,m的最小值=- ![]() .又∵Q在x轴的负半轴上,∴m<0.∴-
.又∵Q在x轴的负半轴上,∴m<0.∴- ![]() ≤m<0.①∵当m<-
≤m<0.①∵当m<- ![]() 时,有且只有△CEP∽△QDP一种情况,∴当m<-
时,有且只有△CEP∽△QDP一种情况,∴当m<- ![]() 时,满足条件的点P有且只有一个.②当-
时,满足条件的点P有且只有一个.②当- ![]() ≤m<0时,存在△CEP∽△QDP或△CEP∽△PDQ两种情况,∴当-
≤m<0时,存在△CEP∽△QDP或△CEP∽△PDQ两种情况,∴当- ![]() ≤m<0时,满足条件的P点有且只有两个
≤m<0时,满足条件的P点有且只有两个
【解析】(1)把A、B、C的坐标代入顶点式,得到抛物线的解析式;(2)由抛物线的对称轴直线,得到CE的值,当△CEP∽△QDP时,得到比例,得到m随x的增大而增大,求出m的取值范围;根据二次函数的解析式得到m的最小值.


科目:初中数学 来源: 题型:
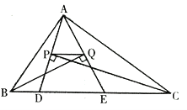
【题目】如图,△ABC的周长为30cm,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=11cm,则DE的长为____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)请你利用上面的结论计算:
299+298+297+…+2+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 为⊙
为⊙ ![]() 的弦,过点
的弦,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() .点
.点 ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)求证:直线 ![]() 是⊙
是⊙ ![]() 的切线;
的切线;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③![]() +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD被两条与边平行的线段EF,GH分割成四个小长方形,EF与GH交于点P,设BF长为a,BG长为b,△GBF的周长为m,
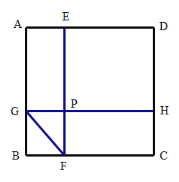
(1)①用含a,b,m的式子表示GF的长为 ;
②用含a,b的式子表示长方形EPHD的面积为 ;
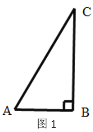
(2)已知直角三角形两直角边的平方和等于斜边的平方,
例如在图1,△ABC中,∠ABC=900,则![]() ,
,
请用上述知识解决下列问题:
①写出a,b,m满足的等式 ;
②若m=1,求长方形EPHD的面积;
③当m满足什么条件时,长方形EPHD的面积是一个常数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的函数图象反映的过程是:李大爷每天早上都到公园锻炼,他从家去公园锻炼一会儿,又去了菜市场后马上回家,其中![]() 表示时间,
表示时间,![]() 表示李大爷离他家的距离。
表示李大爷离他家的距离。
(1)李大爷家到公园的距离是多少千米,他在公园银炼了多少小时;
(2)李大爷从菜市场回家的平均速度;
(3)李大爷从家到菜市场的平均速度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
解:设![]() .
.
方程两边都乘以10,可得![]() .
.
由![]() 和
和![]() ,可得
,可得![]() 即
即![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
解得![]() ,即
,即![]() .
.
填空:将0.![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把小数1.![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )
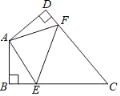
A. 90°B. 80°C. 70°D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com