
【题目】如图,∠AOB是一钢架,且∠O=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH、…,添加的钢管长度都与OE相等,则最多能添加这样的钢管( )

A. 2根 B. 4根 C. 5根 D. 无数根
【答案】C
【解析】分析:因为每根钢管的长度相等,可推出图中的5个三角形都为等腰三角形,再根据外角性质,推出最大的∠0BQ的度数(必须≤90°),就可得出钢管的根数.
详解:如图所示,∠AOB=15°,
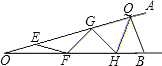
∵OE=FE,
∴∠GEF=∠EGF=15°×2=30°,
∵EF=GF,所以∠EGF=30°
∴∠GFH=15°+30°=45°
∵GH=GF
∴∠GHF=45°,∠HGQ=45°+15°=60°
∵GH=HQ,∠GQH=60°,∠QHB=60°+15°=75°,
∵QH=QB
∴∠QBH=75°,∠HQB=180-75°-75°=30°,
故∠OQB=60°+30°=90°,不能再添加了.
故选C.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组想测量河流的宽度AB,河流两岸AC,BD互相平行,河流对岸有两棵树A和C,且A、C之间的距离是60m,他们在D处测得∠BDC=36°,前行140米后测得∠BPA=45°,请根据这些数据求出河流的宽度.
(结果精确到0.1米,参考数据:tan36°≈0.73,sin36°≈0.59,cos36°≈0.81)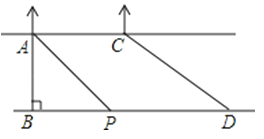
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() (x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.
(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.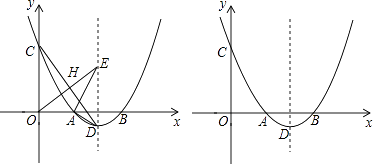
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD. 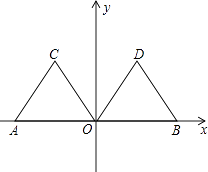
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度;
(2)连结AD,交OC于点E,求∠AEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )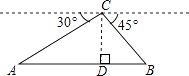
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() +1)米
+1)米
查看答案和解析>>
科目:初中数学 来源: 题型:
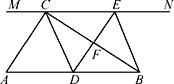
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;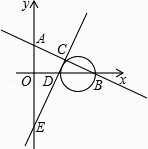
(1)求A、B、C、D、E的坐标;
(2)请用相似三角形的相关知识证明:AB⊥DE;
(3)求△CBD的外接圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com