
 如图所示,直线l是一次函数y=kx+b的图象.
如图所示,直线l是一次函数y=kx+b的图象.分析 (1)结合图象可直接求得答案;
(2)把(1)中所求得的点的坐标代入一次函数解析式可求得k、b的值.
解答 解:
(1)由图象可知图象经过(0,2)和(-3,0)两点,
故答案为:2;-3;
(2)把(1)中两点的坐标代入一次函数解析式可得$\left\{\begin{array}{l}{b=2}\\{-3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=2}\end{array}\right.$,
故答案为:$\frac{2}{3}$;2.
点评 本题主要考查一次函数图象上点的坐标特征,掌握函数图象上的点的坐标满足函数解析式是解题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
 已知,如图,∠ADE=46°,DF平分∠ADE,∠1=23°,求证:DF∥BE.
已知,如图,∠ADE=46°,DF平分∠ADE,∠1=23°,求证:DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
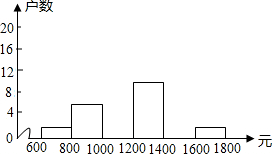 中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图. | 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 45% | |
| 9 | 22.5% | |
| 1600≤x<1800 | 2 | |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1 与∠2的关系一定成立的是( )
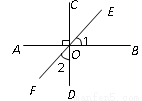
A. 相等 B. 互余 C. 互补 D. 互为对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
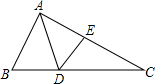 如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°
如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com