
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
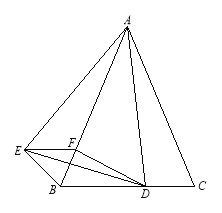
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
【答案】见解析
【解析】
试题分析:根据旋转可得AE=AD,AB=AC,∠EAD=∠BAC,从而得到∠BAE=∠CAD,从而得出△ACD和△ABE全等,从而得出答案;根据题意得出△ABD和△ABE全等,从而得出∠EBF=∠DBF,根据EF∥BC得到∠DBF=∠EFB,从而得到∠EBF=∠EFB,则EB=EF,利用同理得出BD=FD,从而得到菱形.
试题解析:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,∴AE=AD,AB=AC,∠EAD=∠BAC, ∴∠BAE=∠CAD
在△ACD和△ABE中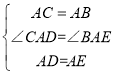 ∴△ACD≌△ABE(SAS) ∴BE=CD;
∴△ACD≌△ABE(SAS) ∴BE=CD;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD, 由(1)可知,△ACD≌△ABE,∴BE=BD=CD,∠BAE=∠BAD
在△ABD和△ABE中,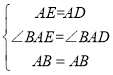 ∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∵EF∥BC, ∴∠DBF=∠EFB, ∴∠EBF=∠EFB, ∴EB=EF,同理BD=FD,∴BD=BE=EF=FD,
∴四边形BDFE为菱形


科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组在研究相似多边形问题时,他们提出了两个观点:
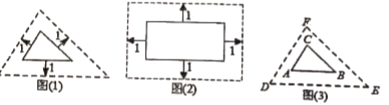
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们的对应边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确,说明理由.
(2)如图3,若![]() 的周长和面积都是24,
的周长和面积都是24,![]() ,将
,将![]() 按图3的方式向外扩张,得到
按图3的方式向外扩张,得到![]() ,它们的对应边间距都为
,它们的对应边间距都为![]() ,
,![]() ,求
,求![]() 的周长和面积.
的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.
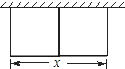
(1)要使鸡场面积最大,鸡场的长度应为多少m?
(2)如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?
比较(1)(2)的结果,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:![]() ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示的一张矩形纸片![]() , 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
, 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
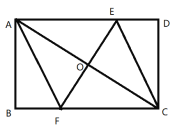
(1)求证:四边形AFCE是菱形;
(2)在线段AC上是否存在一点P,使得![]() ?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() 互相平分;③四边形
互相平分;③四边形![]() 是菱形;④
是菱形;④![]() 。其中正确的个数是( )
。其中正确的个数是( )
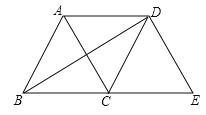
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD⊥AC,对角线AC所在的直线上有两点M、N,使∠MBN=135°,若AD=4,AM=3,则CN的长是_____.
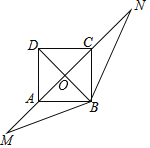
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com