
 如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.
如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由. 分析 此题是一个动点问题,三角板两直角边分别通过点B与点C,则会形成三个直角三角形:依据勾股定理,建立起各边之间的关系,即可解答.
解答 解:能.
理由:设AP=x,则PD=10-x,
在Rt△ABP中,PB2=x2+52,
在Rt△PDC中,PC2=(10-x)2+52,
假设三角板两直角边能分别通过点B与点C,
∵∠BPC是直角三角形,
∴PB2+PC2=BC2,即52+x2+(10-x)2+52=102,解得:x=5(cm).
∴x=5cm时满足PB2+PC2=BC2,
∴三角板两直角边能分别通过点B与点C.
点评 此题考查的是勾股定理的应用,根据题意设出未知数,由勾股定理建立方程,求出x的值是解答此题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | a米 | B. | 80a米 | C. | (a+80)米 | D. | $\frac{a}{80}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.
如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm | B. | 4cm | C. | (3+$\sqrt{3}$)cm | D. | 3$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
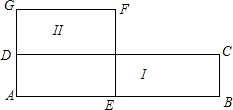 如图,一个长方形ABCD,它的长减少4cm,宽增加2cm,得到一个正方形AEFG,且正方形AEFG的面积与长方形ABCD的面积相等,求长方形ABCD的长与宽.
如图,一个长方形ABCD,它的长减少4cm,宽增加2cm,得到一个正方形AEFG,且正方形AEFG的面积与长方形ABCD的面积相等,求长方形ABCD的长与宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com