
【题目】对于一个两位数,十位数字是![]() ,个位数字是
,个位数字是![]() ,总有
,总有![]() ,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,
,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,![]() ,
,![]() ,所以25和7分别是43的“平方和数”与“平方差数”。
,所以25和7分别是43的“平方和数”与“平方差数”。
(1)76的“平方和数”是_____________,“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”,与它的“平方差数”相等,那么这个数满足什么特征?为什么?(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数_____________,__________.
【答案】(1)85,13;(2)32;(3)31;(4)这个数满足个位是0的特征,理由见解析;(5)55,91.
【解析】
(1)根据“平方和数”,“平方差数”的定义即可求解;
(2)找到两个平方数的差是5的数即可求解;
(3)先把“平方和数”加上“平方差数”,除以2后再求算术平方根可得十位上的数字,进一步可得个位上的数字;
(4)根据“平方和数”与“平方差数”相等,列式计算可得个位数字是0,依此即可求解;
(5)根据“凑整数”的定义列出方程,进一步得到满足条件的数即可求解.
解:(1)76的“平方和数”是72+62=85,“平方差数”是7262=13;
(2)因为3222=5,
所以5可以是,32的“平方差数”;
(3)(10+8)÷2=9,![]() =3,
=3,![]() =1,
=1,
故这个数是31;
(4)若一个数的“平方和数”与它的“平方差数”相等,那么这个数满足个位是0的特征,
理由:因为a2+b2=a2b2,
解得:b=0;
(5)依题意有a2b2=10(ab),
∴(ab)(a+b10)=0,
∴ab=0或a+b10=0.
因为a≥b,
则写出两个这样的凑整数为:55,91.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.
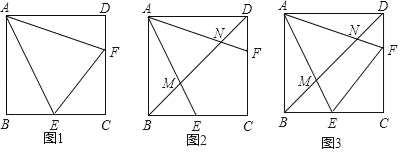
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )

A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形![]() 的顶点都在正方形网格的格点上,将三角形
的顶点都在正方形网格的格点上,将三角形![]() 经过平移后得到三角形
经过平移后得到三角形![]() ,其中点
,其中点![]() 是点
是点![]() 的对应点.
的对应点.

(1)画出平移后得到的三角形![]() ;
;
(2)连接![]() 、
、![]() ,则线段
,则线段![]() 、
、![]() 的关系为______;
的关系为______;
(3)四边形![]() 的面积为______(平方单位).
的面积为______(平方单位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本图形:在RT△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
探索:(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明结论;
(2)连接DE,如图②,试探索线段DE,BD,CD之间满足的等量关系,并证明结论;
联想:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=7,CD=2,则AD的长为 .

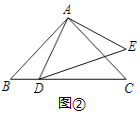
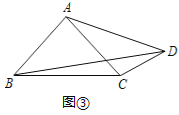
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
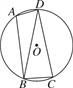
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程3x2-(a-3)x-a=0(a>0).
(1)求证:方程总有两个不相等的实数根;
(2)若方程有一个根大于2,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com