
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线与
的平分线与![]() 的外角平分线交于点
的外角平分线交于点![]() ,连接
,连接![]() ,则
,则![]() 的度数为__________.
的度数为__________.

【答案】![]()
【解析】
首先求得AE也是∠CAB的外角的平分线,根据平角的定义和角平分线的定义求得∠EAB,∠EBA的度数,最后根据三角形的内角和定理即可求得∠AEB.
过点E作EM⊥AC于M,作EN⊥AB于N,EF⊥BC于F,
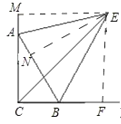
∵E是∠ACB的平分线与∠ABF的平分线的交点,
∴EM=EF,EN=EF,
∴EM=EN,
∴AE是∠CAB的外角的平分线.
∵在Rt△ABC中,∠ACB=90°,∠CAB=40°,
∴∠ABC=50°,∠BAM=180°-40°=140°,∠ABF=180°-50°=130°,
∠BAE=![]() =70°,
=70°,
∵EB是∠ABC的外角的平分线,
∴∠ABE=![]() ,
,
∴∠AEB=180°70°65°=45°.
故答案为:45°.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABO,△A1B1C1,△A2B2C2,…都是正三角形,边长分别为2,22,23,…,且BO,B1C1,B2C2,…都在x轴上,点A,A1,A2,…从左至右依次排列在x轴上方,若点B1是BO中点,点B2是B1C1中点,…,且B为(﹣2,0),则点A6的坐标是( )

A. (61,32![]() ) B. (64,32
) B. (64,32![]() ) C. (125,64
) C. (125,64![]() ) D. (128,64
) D. (128,64![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
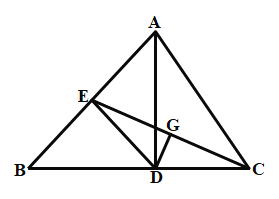
【题目】如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.
(1)求证:DC=BE;
(2)若∠AEC=72°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,C分别在线段NM,NA上,在△ABC中,∠A∶∠ABC∶∠BCA=3∶5∶10,且△ABC≌△MNC,则∠BCM∶∠NBA等于( )

A.1∶2B.1∶3C.1∶4D.1∶5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为12 cm的正三角形,动点P从A向B以2 cm/s匀速运动,同时动点Q从B向C以1 cm/s匀速运动,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t秒,则当△PBQ为直角三角形时,t的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.
(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;
(2)在(1)的条件下,⊙O半径为5.
①若AD为直径,且sinA=![]() ,求BC的长;
,求BC的长;
②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是 ;
(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com