【题目】下图的方格纸中有若干个点，若A、B两点关于过某点的直线对称，这个点可能是（ ）.
A.P1B.P2C.P3D.P4
【答案】C
【解析】
根据两点的对称轴即两点连线的垂直平分线，利用勾股定理分别求出选项中各点到A、B的距离，再根据垂直平分线的性质即可判断.
解：连接P1B，P2A，P3A，P3B，P4B，设正方形的边长为1，P4O=a，如下图所示
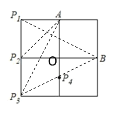
∵A、B两点关于过某点的直线对称
∴此点在AB的垂直平分线上
∴此点到A、B的距离相等
由图可知：P1A=1
根据勾股定理：P1B=
∴P1A≠P1B，故A选项不符合题意；
由图可知：P2B=2
根据勾股定理：P2A=
∴P2B≠P2A，故B选项不符合题意；
根据勾股定理：P3A=
P3B=
∴P3A= P3B，故C选项符合题意；
由图可知P4A=1+a
根据勾股定理：P4B=
当P4A＝P4B时，即1+a=
解得：a=0（与图不符）
∴P4A≠P4B，故D选项不符合题意.
故选C.
科目：初中数学 来源： 题型：
【题目】如图，PA，PB是⊙O的切线，A，B为切点，AC为⊙O的直径，弦BD⊥AC下列结论：①∠P+∠D=180°；②∠COB=∠DAB；③∠DBA=∠ABP；④∠DBO=∠ABP．其中正确的只有（ ）
A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的图象如图所示，有以下结论：①
；②
；③
；④
；⑤
其中所有正确结论的序号是（ ）
A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
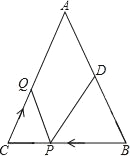
【题目】如图，在△ABC中，∠B＝∠C，AB＝8，BC＝6，点D为AB的中点，点P在线段BC上以每秒2个单位的速度由点B向点C运动，同时点Q在线段CA上以每秒a个单位的速度由点C向点A运动，设运动时间为t（秒）（0≤t≤3）．
（1）用含t的代数式表示线段PC的长；
（2）若点P、Q的运动速度相等，t＝1时，△BPD与△CQP是否全等，请说明理由．
（3）若点P、Q的运动速度不相等，△BPD与△CQP全等时，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（ ）
A．①③ B．②③ C．②④ D．②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=BC,∠ABC=30°，BD平分∠ABC交AC于点D,BC的垂直平分线EF交BC于点E,交BD于点F,若BF=6,则AC的长为____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明同学想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走一段距离时到点D处，侧得∠BDF=65°．若直线AB与EF之间的距离为60米．
（1）设池塘两端的距离AB=x米，试用含x的代数式表示CD的长；
（2）当CD=100米时，求A、B两点的距离（计算结果精确到个位）．（参考数据：sin45°≈0.71，cos65°≈0.42，tan65°≈2.14．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE．
（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=________度；
（2）设
，
．
①如图2，当点在线段BC上移动，则
，
之间有怎样的数量关系？请说明理由；
②当点在直线BC上移动，则，之间有怎样的数量关系？请直接写出你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
