
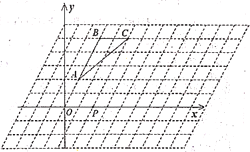
【题目】在如图的菱形网格图中,每个小菱形的边长均为![]() 个单位,且每个小菱形内角中的锐角为60°.
个单位,且每个小菱形内角中的锐角为60°.
(1)直接写出![]() 的三个顶点
的三个顶点![]() 的坐标;
的坐标;
(2)在图中作出![]() 以点
以点![]() 为旋转中心,沿顺时针方向旋转60°后的图形
为旋转中心,沿顺时针方向旋转60°后的图形![]() ;
;
(3)根据(2),请直接写出线段![]() 扫过的面积.
扫过的面积.
【答案】(1)A![]() ,B
,B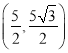 ,C
,C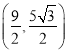 ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)分别过点A,B,C作x轴的垂线,垂足分别为D,E,F,分别过点A,C作y轴的垂线,垂足分别为G,H,根据菱形的性质以及矩形的判定与性质,分别求出各点的坐标即可;
(2)根据旋转的性质,由对应点与对应中心的连线分别相等且夹角为60°分别找出各个对应点,顺次连接即可;
(3)根据线段![]() 扫过的面积=扇形CPC1的面积-扇形APA1的面积求解即可.
扫过的面积=扇形CPC1的面积-扇形APA1的面积求解即可.
解:(1)分别过点A,B,C作x轴的垂线,垂足分别为D,E,F,分别过点A,C作y轴的垂线,垂足分别为G,H,设GA的延长线与BE相交于点M,由题意得,
AG=1,AO=2,AB=3,BC=2,BH=3,∠AOD=∠BAM=60°,
由作图易知四边形OGAD为矩形,四边形MAED为矩形,四边形BEFC为矩形,
∴OD=AG=1,EF=BC=2,AM=DE,AD=ME.
在Rt△AOD中,AD=AO·sin∠AOD=2×sin60°=2×![]() ,∴点A的坐标为(1,
,∴点A的坐标为(1,![]() );
);
在Rt△ABM中,BM=AB·sin∠BAM=3×sin60°=3×![]() ,AM=
,AM=![]() AB=
AB=![]() ,
,
∴OE=OD+DE=0D+AM=1+![]() =
=![]() ,BE=BM+ME=BM+AD=
,BE=BM+ME=BM+AD=![]() ,∴点B的坐标为
,∴点B的坐标为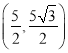 ;
;
OF=OD+DE+EF=OD+AM+BC=1+![]() +2=
+2=![]() ,CF=BE=
,CF=BE=![]() ,∴点C的坐标为
,∴点C的坐标为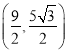 ,
,
故点A,B,C三点的坐标分别为A![]() ,B
,B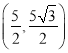 ,C
,C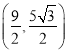 .
.
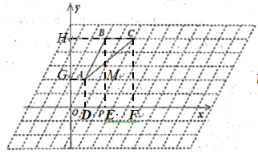
(2)![]() 如图所示:
如图所示:

(3)根据题意可得,
线段![]() 扫过的面积=扇形CPC1的面积-扇形APA1的面积=
扫过的面积=扇形CPC1的面积-扇形APA1的面积=![]() .
.
故所求面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
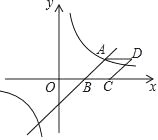
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是( )
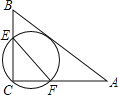
A.![]() B.4.75C.5D.4.8
B.4.75C.5D.4.8
查看答案和解析>>
科目:初中数学 来源: 题型:
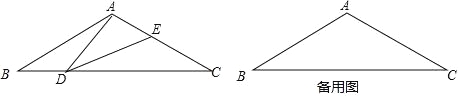
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,抛物线
,抛物线![]() 经过两点
经过两点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() .
.
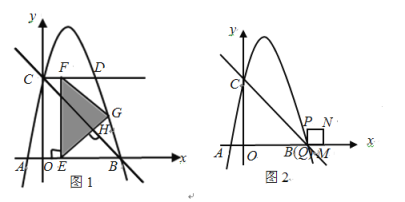
(1)求抛物线的解析式;
(2)如图1,过点![]() 作
作![]() 轴,交抛物线于另一点
轴,交抛物线于另一点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度在线段
个单位长度的速度在线段![]() 上由点
上由点![]() 向点
向点![]() 运动(点
运动(点![]() 不与点
不与点![]() 和点
和点![]() 重合),设运动时间为
重合),设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 轴右侧的抛物线与点
轴右侧的抛物线与点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,正方形![]() ,边
,边![]() 在
在![]() 轴上,点
轴上,点![]() 与点
与点![]() 重合,边长
重合,边长![]() 为
为![]() 个单位长度,将正方形
个单位长度,将正方形![]() 沿射线
沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度平移,时间为
个单位长度的速度平移,时间为![]() 秒,在平移过程中,请写出正方形
秒,在平移过程中,请写出正方形![]() 的边恰好与抛物线有两个交点时
的边恰好与抛物线有两个交点时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙0的直径,AB=10,CD是⊙0的切线,C为切点,交直线AB于E,AD⊥CD于D,AD=2CD.
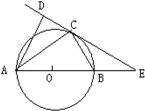
(1)求证:∠CAB=∠CAD;
(2)求CD的长;
(3)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() ,点
,点![]() 是半径
是半径![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 的垂线分别交
的垂线分别交![]() 于点
于点![]() ,交过点
,交过点![]() 的
的![]() 的切线于点
的切线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)如图2,若![]() 是
是![]() 的中点,
的中点,![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=x+4.如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B.C两点,顶点D在正方形内部.
经过B.C两点,顶点D在正方形内部.

(1)写出点M(2,3)任意两条特征线___________________
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com