
分析 (1)原式利用零指数幂、负整数指数幂法则计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算即可得到结果;
(3)原式利用完全平方公式,平方差公式,多项式乘以多项式法则计算即可得到结果;
(4)原式利用积的乘方运算法则,平方差公式计算即可得到结果;
(5)原式利用平方差公式及完全平方公式化简即可得到结果;
(6)原式变形后,利用平方差公式及完全平方公式化简即可得到结果
解答 解:(1)原式=-8+1-9=-16;
(2)原式=9x4y4÷(-$\frac{1}{3}$xy2)•(-x2y)=27x5y3;
(3)原式=4x2-4xy+y2-3x2-3xy+xy+y2-x2+25y2=-6xy+27y2;
(4)原式=(a2-b2)2(a2+b2)2=(a4-b4)2=a8-2a4b4+b8;
(5)原式=4b2-(a-3)2-(a-b)2=4b2-a2+6a-9-a2+2ab-b2=3b2-2a2+6a-9+2ab;
(6)原式=20052-(2005+1)×(2005-1)+672+2×67×33+332=20052-(20052-1)+(67+33)2=20052-20052+1+10000=10001.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | a6÷a2=a3 | B. | $\sqrt{9}$+$\sqrt{2}$=3$\sqrt{2}$ | C. | (a2)3=a6 | D. | (a+b)2=a2+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=6 | B. | a=5,b=5或a=-5,b=-10 | ||
| C. | a=5,b=10 | D. | a=-5,b=-10或a=5,b=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
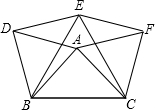 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.
如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
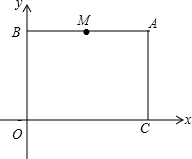 平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).
平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com