
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
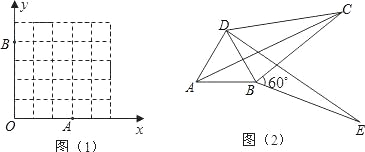
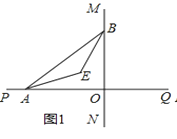
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
(4)若将图2中△ABC绕顶点B按顺时针方向旋转a度(0°<a<90°),得到△DBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
【答案】(1)矩形;正方形(答案不唯一);(2)详见解析:(3,4)或(4,3);(3)详见解析
【解析】试题分析:(1)根据定义和勾股四边形的性质,有矩形或正方形或直角梯形满足题意;
(2)OM=AB知以格点为顶点的M共两个,分别得出答案;
(3)连接CE,证明△BCE是等边三角形,△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形;
(4)连接CE,证明△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形.
试题解析:(1)学过的特殊四边形中是勾股四边形的两种图形的名称:矩形,正方形;
(2)如图1所示:M(3,4),M(4,3);
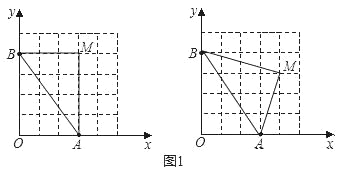
(3)如图2,连接CE,由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60,
∴△CBE为等边三角形,
∴BC=CE,∠BCE=60,
∵∠DCB=30,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形.
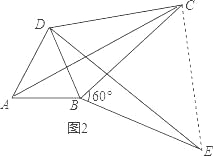
(4)如图3,当∠DCB=![]() ,四边形ABCD是勾股四边形,
,四边形ABCD是勾股四边形,
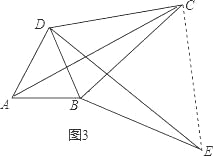
理由:连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=α,
∴∠BCE=∠BEC=90°-![]() ,
,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形


科目:初中数学 来源: 题型:
【题目】数轴上有![]() 、
、![]() 、
、![]() 三点,分别表示有理数
三点,分别表示有理数![]() 、
、![]() 、
、![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,当
个单位的速度向右移动,当![]() 点运动到
点运动到![]() 点时运动停止,设点
点时运动停止,设点![]() 移动时间为
移动时间为![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 点对应的数:_________;
点对应的数:_________;
(2)当![]() 点运动到
点运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位的速度向
个单位的速度向![]() 点运动,
点运动, ![]() 点到达
点到达![]() 点后,再立即以同样的速度返回
点后,再立即以同样的速度返回![]() 点.
点.
①用含![]() 的代数式表示
的代数式表示![]() 点在由
点在由![]() 到
到![]() 过程中对应的数:_________;
过程中对应的数:_________;
②当![]() ______时,动点
______时,动点![]() 、
、![]() 到达同一位置(即相遇);
到达同一位置(即相遇);
③当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小;
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;

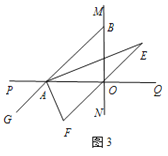
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,在△AEF中,如果有一个角是另一个角的4倍,试求∠ABO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com