

分析 (1)过点P作正方形对边CD、AB的垂线垂足为M、N,可以证明△PMQ≌△BNP,从而得出BP=QP;
(2)过点P作正方形对边CD、AB的垂线垂足为M、N,可以证明△PMQ≌△BNP,从而得出BP=QP;
(3)△PCQ可以成为等腰三角形.当点Q在DC边上时,利用勾股定理可得到x的方程;当点Q在DC的延长线上时,由PQ=CQ,可得到x的方程;当Q与点C重合时,不满足条件;从而可求得满足条件的x的值.
解答 解:
(1)证明:
如图1,过点P作PN⊥AB于N,PN交CD于点M,
在正方形ABCD中,AB∥CD,∠ACD=45°
∴∠PMQ=∠PNB=∠CBN=90°,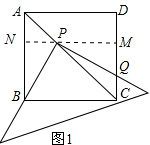
∴CBNM是矩形,
∴CM=BN,
∴△CMP是等腰直角三角形,
∴PM=CM=BN,
∵∠PBN+∠BPN=90°,∠BPN+∠MPQ=90°,
∴∠MPQ=∠PBN,
在△PMQ和△BNP中,
$\left\{\begin{array}{l}{∠MPQ=∠PBN}\\{∠PNB=∠PMQ=90°}\\{BN=PM}\end{array}\right.$,
∴△PMQ≌△BNP,(AAS)
∴BP=QP;
(2)成立;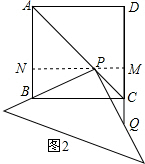
理由:如图2,过点P作PN⊥AB于N,PN交CD于点M,
在正方形ABCD中,AB∥CD,∠ACD=45°
∴∠PMQ=∠PNB=∠CBN=90°,
∴CBNM是矩形,
∴CM=BN,
∴△CMP是等腰直角三角形,
∴PM=CM=BN,
∵∠PBN+∠BPN=90°,∠BPN+∠MPQ=90°,
∴∠MPQ=∠PBN,
在△PMQ和△BNP中,
$\left\{\begin{array}{l}{∠MPQ=∠PBN}\\{∠PNB=∠PMQ=90°}\\{BN=PM}\end{array}\right.$,
∴△PMQ≌△BNP(AAS),
∴BP=QP;
(3)△PCQ可能成为等腰三角形.
①当点Q在边DC上,
由PQ2=CQ2得:(1-$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=(1-$\sqrt{2}$x)2
解得x1=0,x2=$\sqrt{2}$(舍去);
②当点Q在边DC的延长线上时,如图2,
由PC=CQ得:$\sqrt{2}$-x=$\sqrt{2}$x-1,解得x=1.
③当点Q与C点重合,△PCQ不存在.
综上所述,x=0或1时,△PCQ为等腰三角形.
点评 本题主要考查四边形的综合应用,涉及正方形的性质、全等三角形的判定和性质、直角三角形的性质、等腰三角形的性质和勾股定理等知识.在(3)中利用分类讨论思想分别得到关于x的方程是解题的关键.本题考查知识点较多,综合性较强,有一定的难度.搞清楚正方形对角线上点的特点,正方形中的三角形的三边关系,有助于提高解题能力.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax2+bx-$\frac{4}{5}$经过点P(1,-$\frac{4}{5}$)和Q(3,$\frac{8}{5}$).
如图,在平面直角坐标系中,抛物线y=ax2+bx-$\frac{4}{5}$经过点P(1,-$\frac{4}{5}$)和Q(3,$\frac{8}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:判断题
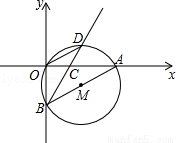
如图,在直角坐标系中,⊙M经过原点O(0,0),点A(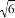 ,0)与点B(0,
,0)与点B(0,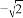 ),点D在劣弧
),点D在劣弧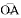 上,连接BD交
上,连接BD交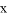 轴于点C,且∠COD=∠CBO.
轴于点C,且∠COD=∠CBO.
(1) 求⊙M的半径;
(2 )求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
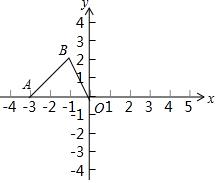 在平面直角坐标系xOy中,以原点O为旋转中心,将△AOB顺时针旋转90°得到△A'OB',其中点A'与点A对应,点B'与点B对应.若点A(-3,0),B(-1,2),则点A'的坐标为(0,3),点B'的坐标为(2,1).
在平面直角坐标系xOy中,以原点O为旋转中心,将△AOB顺时针旋转90°得到△A'OB',其中点A'与点A对应,点B'与点B对应.若点A(-3,0),B(-1,2),则点A'的坐标为(0,3),点B'的坐标为(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com