
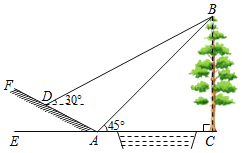
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
【答案】约为15.3米
【解析】
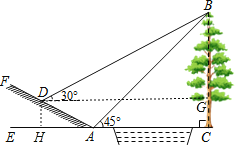
作DH⊥AE于点H,作DG⊥BC于点G,如图,由勾股定理得出![]() .求出DH=CG=3m,则AH=2DH=6m,设BC=xm,则BG=(x﹣3)m,得出
.求出DH=CG=3m,则AH=2DH=6m,设BC=xm,则BG=(x﹣3)m,得出![]() ,解方程即可得出答案.
,解方程即可得出答案.
解:作DH⊥AE于点H,作DG⊥BC于点G,如图,
则四边形DGCH为矩形,
在Rt△ADH中,
∵![]() ,
,
∴AH=2DH,
∵AH2+DH2=AD2,
∴![]() .
.
∴DH=CG=3m,
∴AH=2DH=6m,
设BC=xm,则BG=(x﹣3)m,
在Rt△BAC中,∠BAC=45°,
∴AC=BC=xm,
∴CH=DG=(x+6)m,
在Rt△BDG中,∠BDG=30°,
∵tan30°=![]() ,
,
∴![]() ,
,
解得,x=![]() ≈15.3.
≈15.3.
答:大树BC的高度约为15.3米.


科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,∠ABC=60°,P、Q是对角线BD上的两个动点,点P从点D出发沿BD方向以1cm/s的速度向点B运动,运动终点为B;点Q从点B出发沿着BD的方向以2cm/s的速度向点D运动,运动终点为D.两点同时出发,设运动时间为x(s),以A、Q、C、P为顶点的图形面积为y(cm2),y与x的函数图像如图②所示,根据图像回答下列问题:
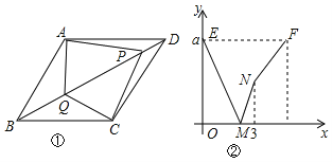
(1)BD= ,a= ;
(2)当x为何值时,以A、Q、C、P为顶点的图形面积为4![]() cm2?
cm2?
(3)在整个运动的过程中,若△AQP为直角三角形,请直接写出符合条件的所有x的值:.
查看答案和解析>>
科目:初中数学 来源: 题型:
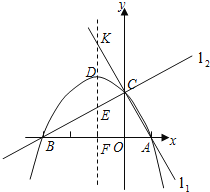
【题目】已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
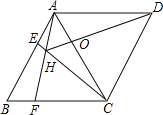
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
(1)当AM=_____________时,△ABM是以AB为底边的等腰三角形;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S与t的函数关系式,并求S最大值.
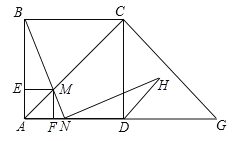
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在四边形ABCD中,![]() ,
,![]() ,
,![]() ,动点P从点B出发沿折线B→A→D→C的方向以1个单位/秒的速度匀速运动,整个运动过程中,△BCP的面积S与运动时间t(秒)的函数关系如图2所示,则AD的长为( )
,动点P从点B出发沿折线B→A→D→C的方向以1个单位/秒的速度匀速运动,整个运动过程中,△BCP的面积S与运动时间t(秒)的函数关系如图2所示,则AD的长为( )
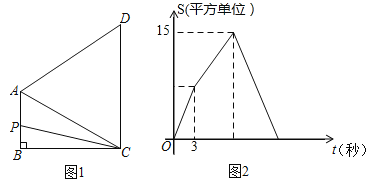
A.5B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
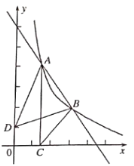
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
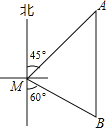
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研发了一种新药,试验药效时发现:1.5小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax2+bx表示;1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=![]() (k>0)表示,部分实验数据如表:
(k>0)表示,部分实验数据如表:
时间x(小时) | 0.2 | 1 | 1.8 | … |
含药量y(微克) | 7.2 | 20 | 12.5 | … |
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(![]() ≈1.41,精确到0.1小时)
≈1.41,精确到0.1小时)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com