Question

善于学习的小敏查资料知道：对应角相等，对应边成比例的两个梯形，叫做相似梯形．他想到“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似”，提出如下两个问题，你能帮助解决吗？
问题一：平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似？
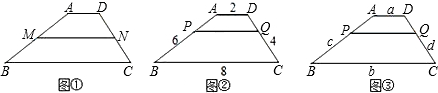
（1）从特殊情形入手探究．假设梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，AD=2，MN是中位线（如图①）．根据相似梯形的定义，请你说明梯形AMND与梯形ABCD是否相似；
（2）一般结论：平行于梯形底边的直线截两腰所得的梯形与原梯形

 

；（填“相似”或“不相似”或“相似性无法确定”．不要求证明）
问题二：平行于梯形底边的直线截两腰所得的两个小梯形是否相似？
（1）从特殊平行线入手探究．梯形的中位线截两腰所得的两个小梯形

 

；（填“相似”或“不相似”或“相似性无法确定”．不要求证明）
（2）从特殊梯形入手探究．同上假设，梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，AD=2，你能找到与梯形底边平行的直线PQ（点P，Q在梯形的两腰上，如图②），使得梯形APQD与梯形PBCQ相似吗？请根据相似梯形的定义说明理由；
（3）一般结论：对于任意梯形（如图③），一定

 

（填“存在”或“不存在”）平行于梯形底边的直线PQ，使截得的两个小梯形相似．若存在，则确定这条平行线位置的条件是

AP

PB

=

 

．（不妨设AD=a，BC=b，AB=c，CD=d．不要求证明）

Answer 1

分析：两个梯形相似，因而两个梯形的对应腰的相等，对应底的比相等；这个图形中判定相似要同时满足这几个条件．反之，若相似则两个梯形的对应腰的相等，对应底的比相等．

解答：解：问题一：（1）两个梯形的腰相等，
即腰的比是1：2，而上底的比是1：1，
因而这两个梯形一定不相似；
（2）不相似．
问题二：（1）不相似；
（2）梯形APQD与梯形PBCQ相似，
∴

AD

PQ

=

PQ

BC

，即

2

PQ

=

PQ

8

解得：PQ=4．
∵

AP

PB

=

AD

PQ

=

2

4

=

1

2

．
又∵AP+PB=6，
∴AP=2
（3）如果梯形APQD∽梯形PBCQ，
则

AD

PQ

=

PQ

BC

，

AP

PB

=

AD

PQ

，
∵AD=a，BC=b，
∴PQ=

AD•BC

=

ab

，
∴

AP

PB

=

a

ab

=

ab

b

．

点评：本题考查了多边形相似的性质，对应边的比相等，反之，相似图形的判定方法是对应角相等，对应边的比相等．