
【题目】如图是抛物线![]() 图像的一部分,抛物线的项点坐标是A(1,3),与
图像的一部分,抛物线的项点坐标是A(1,3),与![]() 轴的一个交点B(4,0),直线
轴的一个交点B(4,0),直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:①
两点,下列结论:①![]() :②
:②![]()
![]() ;③方程
;③方程![]() 有两个相等的实数根:④当
有两个相等的实数根:④当![]() 时,有
时,有![]() ;⑤抛物线与
;⑤抛物线与![]() 轴的另一个交点是(-1,0),其中正确的是( )
轴的另一个交点是(-1,0),其中正确的是( )

A.①②③B.①③④C.①③⑤D.②④⑤
【答案】B
【解析】
根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据顶点坐标对③进行判断;根据函数图象得当1<x<4时,一次函数图象在抛物线下方,则可对④进行判断;根据抛物线的对称性对⑤进行判断.
∵抛物线的顶点坐标A(1,3),
∴抛物线的对称轴为直线x=![]() =1,
=1,
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以④正确.
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(2,0),所以⑤错误;
故选:B.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】请阅读下列解题过程:
解一元二次不等式:x2-3x>0.
解:x(x-3)>0,
∴![]() 或
或![]() ,
,
解得x>3或x<0.
∴一元二次不等式x2-3x>0的解集为x<0或x>3.
结合上述解题过程回答下列问题:
(1)上述解题过程渗透的数学思想为 ;
(2)一元二次不等式x2-3x<0的解集为 ;
(3)请用类似的方法解一元二次不等式:x2-2x-3<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,A(6,0)、C(0,![]() )、D(0,
)、D(0,![]() ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
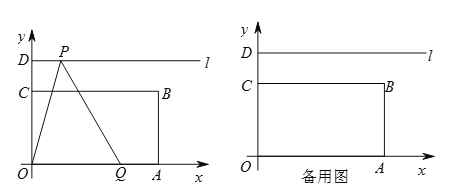
(1)①点B的坐标是 ;
②当点Q与点A重合时,点P的坐标为 ;
(2)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式及相应的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.
x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.

(1)一动点P从点E出发,沿适当的路径运动到直线BC上的点F,再沿适当的路径运动到点D处.当P的运动路径最短时,求此时点F的坐标及点P所走最短路径的长;
(2)点E沿直线y=3水平向右运动得点E',平面内是否存在点M使得以D、B、M、E'为顶点的四边形为菱形,若存在,请直接写出点E′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,数据整理过程如下,请完成下面数据整理中的问题:
(1)收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m= ,n= ;
(3)分析数据
①若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人;
②现从甲班指定的3名学生(1男2女),乙班指定的2名学生(1男1女)中分别抽取1名学生去参加身体素质拓展训练,用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
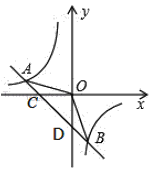
根据以往所学的函数知识以及本题的条件,你能提出求解什么问题?并解决这些问题(至少三个问题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形的土地,它的一条边BC=100米,DC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分別在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是_____平方米.
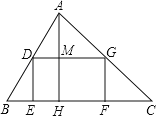
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,点O在AB上,以点O为圆心,OA为半径的圆与BC相切与点D,与AC相交与点E,若CD=6,则CE=__.
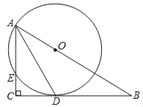
查看答案和解析>>
科目:初中数学 来源: 题型:
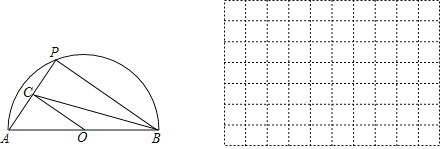
【题目】如图,P是半圆弧![]() 上一动点,连接PA、PB,过圆心O作
上一动点,连接PA、PB,过圆心O作![]() 交PA于点C,连接
交PA于点C,连接![]() 已知
已知![]() ,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
![]() 说明:补全表格时相关数据保留一位小数
说明:补全表格时相关数据保留一位小数![]()
![]() 建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:直接写出
结合画出的函数图象,解决问题:直接写出![]() 周长C的取值范围是______.
周长C的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com