
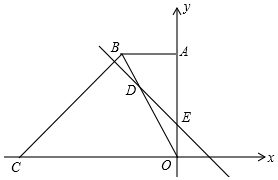
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±½ĒĢŻŠĪOABCµÄ±ßOC”¢OA·Ö±šÓėxÖį”¢yÖįÖŲŗĻ£¬AB”ĪOC£¬”ĻAOC=90”ć£¬”ĻBCO=45”ć£¬BC=$12\sqrt{2}$£¬µćCµÄ×ų±źĪŖ£Ø-18£¬0£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±½ĒĢŻŠĪOABCµÄ±ßOC”¢OA·Ö±šÓėxÖį”¢yÖįÖŲŗĻ£¬AB”ĪOC£¬”ĻAOC=90”ć£¬”ĻBCO=45”ć£¬BC=$12\sqrt{2}$£¬µćCµÄ×ų±źĪŖ£Ø-18£¬0£©£®·ÖĪö £Ø1£©¹żB×÷BF”ĶxÖįÓŚµćF£¬ŌŚRt”÷BCFÖŠæÉĒóµĆBFŗĶCF£¬ŌņæÉĒóµĆBµćµÄ×ų±ź£»
£Ø2£©¹żD×÷DG”ĶyÖįÓŚµćG£¬ÓÉ”÷ODG”×”÷OBAæÉĒóµĆOGŗĶDG£¬ŌņæÉĒóµĆDµć×ų±ź£¬ĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆÖ±ĻßDEµÄ½āĪöŹ½£»
£Ø3£©½įŗĻÖ±ĻßDEµÄ½āĪöŹ½æÉÉč³öPµć×ų±ź£¬±ķŹ¾³öPE”¢POŗĶOEµÄ³¤£¬ĄūÓƵČŃüČż½ĒŠĪµÄŠŌÖŹæɵƵ½¹ŲÓŚPµć×ų±źµÄ·½³Ģ£¬æÉĒóµĆPµć×ų±ź£®
½ā“š ½ā£ŗ
£Ø1£©ČēĶ¼1£¬¹żµćB×÷BF”ĶxÖįÓŚµćF£¬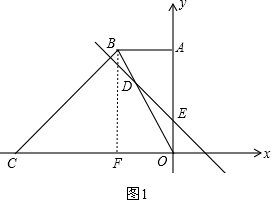
ŌŚRt”÷BCFÖŠ£¬
”ß”ĻBCO=45”ć£¬BC=12$\sqrt{2}$£¬
”ąBF=CF=12£¬
”ßC£Ø-18£¬0£©£¬
”ąOF=AB=6£¬
”ąB£Ø-6£¬-12£©£»
£Ø2£©ČēĶ¼2£¬¹żµćD×÷DG”ĶyÖįÓŚµćG£¬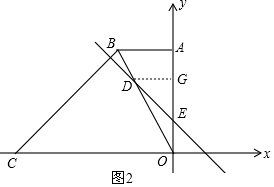
”ßAB”ĪDG£¬
”ą”÷ODG”×”÷OBA£¬
”ą$\frac{DG}{AB}$=$\frac{OD}{OB}$=$\frac{OG}{OA}$=$\frac{2}{3}$£¬
”ßAB=6£¬OA=12£¬
”ąDG=4£¬OG=8£¬
”ąD£Ø-4£¬8£©£¬ĒŅE£Ø0£¬4£©£¬
ÉčÖ±ĻßDE½āĪöŹ½ĪŖy=kx+b£Øk”Ł0£©£¬
”ą$\left\{\begin{array}{l}{-4k+b=8}\\{b=4}\end{array}\right.$£¬½āµĆ$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$£¬
”ąÖ±ĻßDEµÄ½āĪöŹ½ĪŖy=-x+4£»
£Ø3£©”ßµćPŌŚÖ±ĻßDEÉĻ£¬
”ąæÉÉčP£Øt£¬-t+4£©£¬
”ßE£Ø0£¬4£©£¬O£Ø0£¬0£©£¬
”ąPE=$\sqrt{{t}^{2}+£Ø-t+4-4£©^{2}}$=$\sqrt{2}$|t|£¬PO=$\sqrt{{t}^{2}+£Ø-t+4£©^{2}}$=$\sqrt{2{t}^{2}-8t+16}$£¬EO=4£¬
”ß”÷OPEĪŖ½ÖŃüČż½ĒŠĪ£¬
”ąÓŠPE=PO”¢PE=OEŗĶPO=EOČżÖÖĒéæö£¬
¢Łµ±PE=POŹ±£¬Ōņ$\sqrt{2}$|t|=$\sqrt{2{t}^{2}-8t+16}$£¬½āµĆt=2£¬“ĖŹ±Pµć×ų±źĪŖ£Ø2£¬2£©£»
¢Śµ±PE=OEŹ±£¬Ōņ$\sqrt{2}$|t|=4£¬½āµĆt=”Ą2$\sqrt{2}$£¬“ĖŹ±Pµć×ų±źĪŖ£Ø2$\sqrt{2}$£¬4+2$\sqrt{2}$£©»ņ£Ø-2$\sqrt{2}$£¬4-2$\sqrt{2}$£©£»
¢Ūµ±PO=EOŹ±£¬Ōņ$\sqrt{2{t}^{2}-8t+16}$=4£¬½āµĆt=0£ØÓėEÖŲŗĻ£¬ÉįČ„£©»ņt=4£¬“ĖŹ±Pµć×ų±źĪŖ£Ø4£¬0£©£»
×ŪÉĻæÉÖŖ“ęŌŚĀś×ćĢõ¼žµÄµćP£¬Ęä×ų±źĪŖ£Ø2£¬2£©»ņ£Ø2$\sqrt{2}$£¬4+2$\sqrt{2}$£©»ņ£Ø-2$\sqrt{2}$£¬4-2$\sqrt{2}$£©»ņ£Ø4£¬0£©£®
µćĘĄ ±¾ĢāĪŖŅ»“ĪŗÆŹżµÄ×ŪŗĻÓ¦ÓĆ£¬Éę¼°¹“¹É¶ØĄķ”¢“ż¶ØĻµŹż·Ø”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢µČŃüČż½ĒŠĪµÄŠŌÖŹ”¢·½³ĢĖ¼Ļė¼°·ÖĄąĢÖĀŪĖ¼ĻėµČÖŖŹ¶£®ŌŚ£Ø1£©ÖŠ¹¹ŌģÖ±½ĒČż½ĒŠĪ£¬ĒóµĆBµ½Į½×ų±źÖįµÄ¾ąĄėŹĒ½āĢāµÄ¹Ų¼ü£¬ŌŚ£Ø2£©ÖŠ¹¹ŌģĻąĖĘČż½ĒŠĪĒóµĆDµć×ų±źŹĒ½āĢāµÄ¹Ų¼ü£¬ŌŚ£Ø3£©ÖŠÓĆPµć×ų±ź±ķŹ¾³öPEŗĶOPµÄ³¤ŹĒ½āĢāµÄ¹Ų¼ü£®±¾Ģāæ¼²éÖŖŹ¶µć½Ļ¶ą£¬×ŪŗĻŠŌ½ĻĒ棬ÄѶȏŹÖŠ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 3x2-$\frac{2}{x}$=0 | B£® | x2+2x+3 | C£® | x£Øx-3£©=0 | D£® | £Ø2x-1£©2=4x£Øx-2£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com