
分析 (1)因式分解法求解可得;
(2)因式分解法求解即可得;
(3)整理成一般式,因式分解法求解;
(4)因式分解法求解.
解答 解:(1)∵3x2+5x-2=0,
∴(x+2)(3x-1)=0,
则x+2=0或3x-1=0,
解得:x=-2或x=$\frac{1}{3}$;
(2)∵3x(x+3)-(x+3)(x-3)=0,
∴(x-3)(3x-x-3)=0,即(x-3)(2x-3)=0,
则x-3=0或2x-3=0,
解得:x=3或x=$\frac{3}{2}$;
(3)整理成一般式得x2+4x-12=0,
∴(x-2)(x+6)=0,
则x-2=0或x+6=0,
解得:x=2或x=-6;
(4)∵x(3x-5)-2(3x-5)=0,即(3x-5)(x-2)=0,
∴3x-5=0或x-2=0,
解得:x=$\frac{5}{3}$或x=2.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
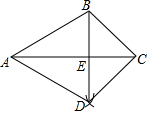 如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角三角形纸板ABP的直角顶点P在直线l上,AP=3,BP=4,分别作AC⊥l于点C,BD⊥l于点D,若将三角形纸板在平面内绕点P旋转(点C、D、P互不重合),请直接写出旋转过程中线段CD、AC、BD的数量关系.
如图,直角三角形纸板ABP的直角顶点P在直线l上,AP=3,BP=4,分别作AC⊥l于点C,BD⊥l于点D,若将三角形纸板在平面内绕点P旋转(点C、D、P互不重合),请直接写出旋转过程中线段CD、AC、BD的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
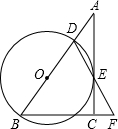 如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.
如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$或$-\frac{5}{4}$ | B. | $\frac{3}{4}$或$\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
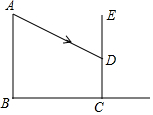 如图,一位同学想利用建筑物的影子测量建筑物AB的高度,他在某一时刻测得直立的标杆高为1m时,影长为1.2m,他立即又测量建筑物的影子,因建筑物AB靠近另一个建筑物CE,所以AB的影子没有完全落在地上,一部分影子落在墙上,他测得地上部分的影子长BC为7.2m,又测得墙上部分的影子高CD为1.2m,请你帮他计算建筑物AB的高度.
如图,一位同学想利用建筑物的影子测量建筑物AB的高度,他在某一时刻测得直立的标杆高为1m时,影长为1.2m,他立即又测量建筑物的影子,因建筑物AB靠近另一个建筑物CE,所以AB的影子没有完全落在地上,一部分影子落在墙上,他测得地上部分的影子长BC为7.2m,又测得墙上部分的影子高CD为1.2m,请你帮他计算建筑物AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
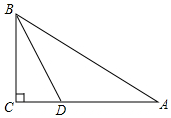 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )| A. | 5 cm | B. | 4 cm | C. | 3 cm | D. | 2 cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com