
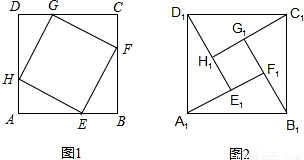
 在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于
在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于| x2+(4-x)2 |


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
| A、A | B、B | C、C | D、D |
查看答案和解析>>
科目:初中数学 来源: 题型:
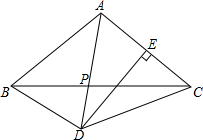 如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD
如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD查看答案和解析>>
科目:初中数学 来源: 题型:
 某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.
某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com