
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm .当点Q到达顶点C时,P,Q同时停止运动.设P, Q两点运动时间为t秒.

(1)当x为何值时,PQ∥BC ?
(2)设四边形PQCB的面积为y,求y关于t的函数解析式;
(3)四边形PQCB的面积与△APQ面积比为3:2?若能,求出此时t的值;若不能,请说明理由;
(4)当x为何值时,△AEQ为等腰三角形?
)(1) ;(2)y=
;(2)y= t2-8t+24;(3)四边形PQCB面积能是△ABC面积的
t2-8t+24;(3)四边形PQCB面积能是△ABC面积的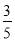 ,此时t的值为5-
,此时t的值为5- ;(4)当t为
;(4)当t为 秒、
秒、 秒、
秒、 秒时,△AEQ为等腰三角形.
秒时,△AEQ为等腰三角形.
【解析】
试题分析:(1)先在Rt△ABC中,由勾股定理求出AB=10,再由BP=t,AQ=2t,得出AP=10-t,然后由PQ∥BC,根据平行线分线段成比例定理得出 ,列出比例式
,列出比例式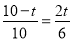 ,求解即可;
,求解即可;
(2)根据S四边形PQCB=S△ACB-S△APQ= AC•BC-
AC•BC- AP•AQ•sinA,即可得出y关于t的函数关系式;
AP•AQ•sinA,即可得出y关于t的函数关系式;
(3)根据四边形PQCB面积是△ABC面积的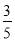 ,列出方程
,列出方程 t2-8t+24=
t2-8t+24=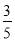 ×24,解方程即可;
×24,解方程即可;
(4)△AEQ为等腰三角形时,分三种情况讨论:①AE=AQ;②EA=EQ;③QA=QE,每一种情况都可以列出关于t的方程,解方程即可.
试题解析:(1)Rt△ABC中,∵∠C=90°,BC=8cm,AC=6cm,
∴AB=10cm.
∵BP=t,AQ=2t,
∴AP=AB-BP=10-t.
∵PQ∥BC,
∴ ,
,
∴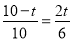 ,
,
解得t= ;
;
(2)∵S四边形PQCB=S△ACB-S△APQ= AC•BC-
AC•BC- AP•AQ•sinA
AP•AQ•sinA
∴y= ×6×8-
×6×8- ×(10-2t)•2t•
×(10-2t)•2t• =24-
=24- t(10-2t)=
t(10-2t)= t2-8t+24,
t2-8t+24,
即y关于t的函数关系式为y= t2-8t+24;
t2-8t+24;
(3)四边形PQCB面积能是△ABC面积的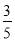 ,理由如下:
,理由如下:
由题意,得
 t2-8t+24=
t2-8t+24=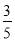 ×24,
×24,
整理,得t2-10t+12=0,
解得t1=5- ,t2=5+
,t2=5+ (不合题意舍去).
(不合题意舍去).
故四边形PQCB面积能是△ABC面积的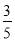 ,此时t的值为5-
,此时t的值为5- ;
;
(4)△AEQ为等腰三角形时,分三种情况讨论:
①如果AE=AQ,那么10-2t=2t,解得t= ;
;
②如果EA=EQ,那么(10-2t)× =t,解得t=
=t,解得t= ;
;
③如果QA=QE,那么2t× =5-t,解得t=
=5-t,解得t= .
.
故当t为 秒、
秒、 秒、
秒、 秒时,△AEQ为等腰三角形.
秒时,△AEQ为等腰三角形.
考点:相似形综合题.


科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:填空题
已知x=-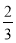 是方程2x+a=
是方程2x+a= +3a的解,则关于m的方程:2am+7=a(3-m)的解,m= 。
+3a的解,则关于m的方程:2am+7=a(3-m)的解,m= 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
如图,一次函数y1=2x+1的图像与反比例函数y2=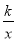 (k为常数,且
(k为常数,且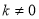 )的图像都经过点A(m,3)
)的图像都经过点A(m,3)
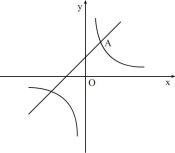
(1)求点A的坐标及反比例函数的表达式
(2)结合图像直接比较:当x>0时,y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:解答题
如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)
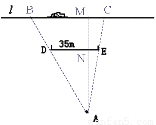
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市八年级上学期期末模拟数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.﹣3的倒数是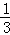
B.﹣2的绝对值是﹣2
C.﹣(﹣5)的相反数是﹣5
D.x取任意实数时, 都有意义
都有意义
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com