

 t2+t(0<t<2),
t2+t(0<t<2), t2﹣t(2<t≤4).
t2﹣t(2<t≤4). ,H1(
,H1( ,
, ),
), ,H2(10﹣4
,H2(10﹣4 ,4).
,4). ,
,


 t,AF=CQ=4﹣t,
t,AF=CQ=4﹣t, PE•PF=
PE•PF= ×
× t(4﹣2t)=t﹣
t(4﹣2t)=t﹣ t2,
t2, t2+t(0<t<2),
t2+t(0<t<2), PE•PF=
PE•PF= ×
× t(2t﹣4)=
t(2t﹣4)= t2﹣t(2<t≤4).
t2﹣t(2<t≤4). ,H1(
,H1( ,
, ),
), ,H2(10﹣4
,H2(10﹣4 ,4).
,4).

科目:初中数学 来源:不详 题型:解答题
 .延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3. (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 恒过定点
恒过定点 .
. 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;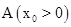 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.第一、二、三象限 | B.第一、二、四象限 |
| C.第一、三、四象限 | D.第二、三、四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com