
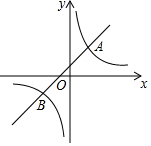
 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.分析 (1)根据A(2,3),可得m的值,进而得到n的值,再根据待定系数法,即可得出一次函数解析式;
(2)先求得C(0,1),得到OC=1,再根据根据题意得:S△ABP=$\frac{1}{2}$PC×2+$\frac{1}{2}$PC×3=5,进而得出PC=2,据此可得点P的坐标.
解答 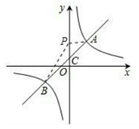 解:(1)∵点A(2,3)在y=mx-1上,
解:(1)∵点A(2,3)在y=mx-1上,
∴m=6,
∴反比例函数解析式为y=6x-1;
又∵点B(-3,n)在y=6x-1上,
∴n=-2,
∴点B的坐标为(-3,-2),
把A(2,3)和B(-3,-2)两点的坐标代入一次函数y=kx+b得
2k+b=3,-3k+b=-2,
解得k=1,b=1,
∴一次函数的解析为y=x+1.
(2)对于一次函数y=x+1,令x=0,则y=1,
即C(0,1),
∴OC=1,
根据题意得:S△ABP=$\frac{1}{2}$PC×2+$\frac{1}{2}$PC×3=5,
解得:PC=2,
∴OP=3或1,
∴P(0,3)或(0,-1).
点评 本题主要考查了一次函数与反比例函数交点问题,解题时注意:一次函数与反比例函数交点坐标同时满足一次函数与反比例函数解析式.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
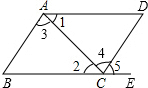 如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B;④AD∥BE,且∠D=∠B;⑤∠1+∠3+∠B=180°.其中能说明AB∥DC的条件有( )
如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B;④AD∥BE,且∠D=∠B;⑤∠1+∠3+∠B=180°.其中能说明AB∥DC的条件有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com