
分析 画出M={x2+2,$\frac{3}{x}$(x>0),-$\frac{3}{x}$(x<0)}的图象,由一次函数y=kx+b与M只有一个交点,可知直线过M图象的转折点(最低点),再结合点(-2,0)利用待定系数法即可求出k值.
解答 解:根据题意画出图形,如图所示.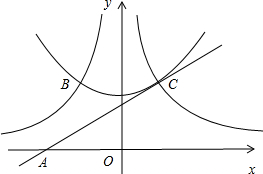
令y=x2+2=$\frac{3}{x}$,或y=x2+2=-$\frac{3}{x}$,
解得:x=-1,或x=1,
即点B的坐标为(-1,3),点C的坐标为(1,3).
结合题意可知:$\left\{\begin{array}{l}{0=-2k+b}\\{3=-k+b}\end{array}\right.$或$\left\{\begin{array}{l}{0=-2k+b}\\{3=k+b}\end{array}\right.$,
解得:k=3或k=1.
故答案为:1或3.
点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是求出一次函数过的另外一点的坐标.本题属于中档题,难度不大,解决该题型题目时,首先根据新定义确定函数M的图象,再结合一次函数的性质结合题意找出一次函数经过的点的位置,求出点的坐标,结合待定系数法即可求出结论.


科目:初中数学 来源: 题型:解答题
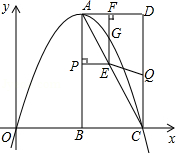 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
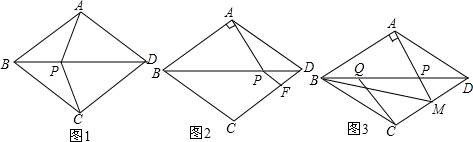 如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,
如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折得△CBD,点P是线段BD上一点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{BC}{AB}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BC}{AC}$ | D. | $\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.
已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com