
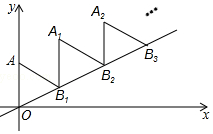
 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019). 分析 根据题意得出直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,进而得出A,A1,A2,A3坐标,进而得出坐标变化规律,进而得出答案.
解答  解:过B1向x轴作垂线B1C,垂足为C,
解:过B1向x轴作垂线B1C,垂足为C,
由题意可得:A(0,2),AO∥A1B1,∠B1OC=30°,
∴CO=OB1cos30°=$\sqrt{3}$,
∴B1的横坐标为:$\sqrt{3}$,则A1的横坐标为:$\sqrt{3}$,
连接AA1,可知所有三角形顶点都在直线AA1上,
∵点B1,B2,B3,…都在y=$\frac{\sqrt{3}}{3}$x上,AO=2,
∴直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,
∴y=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$+2=3,
∴A1($\sqrt{3}$,3),
同理可得出:A2的横坐标为:2$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$+2=4,
∴A2(2$\sqrt{3}$,4),
∴A3(3$\sqrt{3}$,5),
…
A2017(2017$\sqrt{3}$,2019).
故答案为:(2017$\sqrt{3}$,2019).
点评 本题为规律型题目,利用等边三角形和直角三角形的性质求得B1的坐标,进而求得A1的坐标,从而总结出点的坐标的规律是解题的关键.


科目:初中数学 来源: 题型:解答题
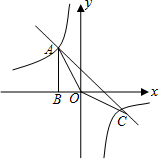 如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$
如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
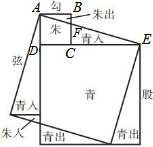 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
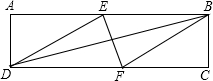 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 污水处理器型号 | A型 | B型 |
| 处理污水能力(吨/月) | 240 | 180 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com