
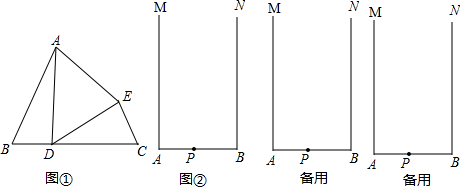
���� ��1�����ȸ��ݡ�B=��C��BD=CE��AB=DC���ж���ABD��DCE���ó�AB=DC�������õ���ADEΪ���������Σ��ڸ��ݡ�ABD�ա�DCE���ó���BAD=��CDE���ٸ��ݡ�ADC=��B+��BAD����ADC=��ADE+��EDC���õ���ADE=��B=60�㣬����ж�������ADEΪ�ȱ������Σ�
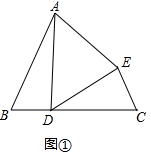
��2��������������ۣ���CPDΪֱ�Ƕ��㣻��PCD��ֱ�Ƕ��㣻��PDC��ֱ�Ƕ��㣬�ֱ���л�ͼ���ɣ���һ�������ʹ��AP=BD��BP=AC���ڶ��������ʹ��AC=AB��CE=AP��BD=AE�������������ʹ��BD=AB��DF=BP��AC=BF��
���  �⣺��1����֤�����ߡ�B=��C��BD=CE��AB=DC��
�⣺��1����֤�����ߡ�B=��C��BD=CE��AB=DC��
���ABD��DCE��
��AB=DC��
���ADE����������
�ڡߡ�ABD�ա�DCE��
���BAD=��CDE��
�ߡ�ADC�ǡ�ABD����ǣ�
���ADC=��B+��BAD��
�ߡ�ADC=��ADE+��EDC��
�֡ߡ�BAD=��CDE��
���ADE=��B=60�㣬
�������ADEΪ�ȱ������Σ�
��2�������ֽ������ͼ��ʾ��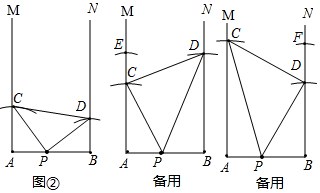
���� ������Ҫ�����˵���ֱ�������ε����ʣ��ȱ������ε��ж��������Լ�ȫ�������ε��ж������ʵ��ۺ�Ӧ�ã��������Ĺؼ�������ȫ�������ε��ж�����������ʱע���������˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �������ϣ���A�����ƶ�1����λ�õ���B����B�����ƶ�2����λ�õ���C����A��B��C�ֱ��ʾ������a��b��c��A��B��C�����������ϵ�λ����ͼ��ʾ��a��b��c�������ij˻�Ϊ�����������������ĺ������е�һ������ȣ���a��ֵΪ��������
�������ϣ���A�����ƶ�1����λ�õ���B����B�����ƶ�2����λ�õ���C����A��B��C�ֱ��ʾ������a��b��c��A��B��C�����������ϵ�λ����ͼ��ʾ��a��b��c�������ij˻�Ϊ�����������������ĺ������е�һ������ȣ���a��ֵΪ��������| A�� | -$\frac{3}{2}$ | B�� | -$\frac{1}{2}$ | C�� | -$\frac{1}{2}$��-$\frac{3}{2}$ | D�� | -$\frac{3}{2}$��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��9 | B�� | -4��9 | C�� | 2��9 | D�� | 2��-9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
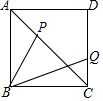 ��ͼ��������ABCD�У���֪AB=2������P��Q�ֱ���AC��CD�ϣ���AP=CQ����BP+BQ��2����Сֵ��8+4$\sqrt{2}$��
��ͼ��������ABCD�У���֪AB=2������P��Q�ֱ���AC��CD�ϣ���AP=CQ����BP+BQ��2����Сֵ��8+4$\sqrt{2}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com