
”¾ĢāÄæ”æѧŠ£Ķ³³ļ°²ÅÅ“óæĪ¼äĢåÓż»ī¶Æ£¬ŌŚø÷°ąĖ껜єȔĮĖŅ»²æ·Öѧɜ£¬·Ö³ÉĖÄĄą»ī¶Æ£ŗ”°ĢųÉž”±”¢”°ÓšĆ«Ēņ”±”¢”°Ę¹ÅŅĒņ”±”¢”°ĘäĖū”±½ųŠŠµ÷²é£¬ÕūĄķŹÕ¼Æµ½µÄŹż¾Ż£¬»ęÖĘ³ÉČēĶ¼µÄĮ½·łĶ³¼ĘĶ¼£®
£Ø1£©Ń§Š£²ÉÓƵĵ÷²é·½Ź½ŹĒ””””””””””””£»Ń§Š£ŌŚø÷°ąĖ껜єȔĮĖ””””””””””””Ćūѧɜ£»
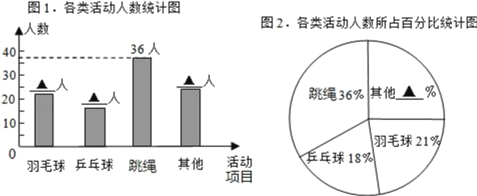
£Ø2£©²¹Č«Ķ³¼ĘĶ¼ÖŠµÄŹż¾Ż£ŗӚƫĒņ””””””””ČĖ”¢Ę¹ÅŅĒņ””””””””””ČĖ”¢ĘäĖū””””””””””””%£»
£Ø3£©øĆŠ£¹²ÓŠ900Ćūѧɜ£¬Ēė¹Ą¼ĘĻ²»¶”°ĢųÉž”±µÄѧɜČĖŹż£®
”¾“š°ø”æ£Ø1£©³éŃłµ÷²é£¬100£»£Ø2£©21£¬18£¬![]() £»£Ø3£©Ļ²»¶”°ĢųÉž”±µÄѧɜČĖŹżĪŖ324ČĖ£®
£»£Ø3£©Ļ²»¶”°ĢųÉž”±µÄѧɜČĖŹżĪŖ324ČĖ£®
”¾½āĪö”æ
£Ø1£©øł¾Ż”°ŌŚø÷°ąĖ껜єȔĮĖŅ»²æ·Öѧɜ”±æÉÖŖŹĒ³éŃłµ÷²é£¬Č»ŗóĄūÓĆ”°ĢųÉž”±µÄČĖŹżĪŖ36ČĖ£¬²¢ĒŅÕ¼×ÜČĖŹżµÄ![]() ½ųŅ»²½¼ĘĖć³éČ”ČĖŹż¼“æÉ£»
½ųŅ»²½¼ĘĖć³éČ”ČĖŹż¼“æÉ£»
£Ø2£©·Ö±šÓĆ”°ÓšĆ«Ēņ”±”¢”°Ę¹ÅŅĒņ”±Õ¼µÄ°Ł·Ö±Č³ĖŅŌ³éČ”ČĖŹż½ųŠŠ¼ĘĖć³öĻą¶ŌÓ¦ČĖŹż£¬Č»ŗóÓĆ1¼õČ„”°ÓšĆ«Ēņ”±”¢”°Ę¹ÅŅĒņ”±”¢”°ĢųÉž”±µÄ°Ł·Ö±Č¼“æÉµĆ³ö”°ĘäĖū”±µÄ°Ł·Ö±Č£»
£Ø3£©ĄūÓĆŃł±¾¹Ą¼Ę×ÜĢ壬ÓĆ900³ĖŅŌ”°ĢųÉž”±µÄ°Ł·Ö±Č½ųŅ»²½¼ĘĖć¼“æÉ.
£Ø1£©ÓÉ”°ŌŚø÷°ąĖ껜єȔĮĖŅ»²æ·Öѧɜ”±æÉÖŖŹĒ³éŃłµ÷²é£¬
ÓÖ”ß ![]() £¬
£¬
”ą³éČ”×ÜČĖŹżĪŖ100ČĖ£¬
¹Ź“š°øĪŖ£ŗ³éŃłµ÷²é£¬100£»
£Ø2£©ÓÉ£Ø1£©æÉµĆ³éČ”×ÜČĖŹżĪŖ100ČĖ£¬
”ą”°ÓšĆ«Ēņ”±ČĖŹżĪŖ£ŗ![]() £ØČĖ£©£¬
£ØČĖ£©£¬
”°Ę¹ÅŅĒņ”±ČĖŹżĪŖ£ŗ![]() £ØČĖ£©£¬
£ØČĖ£©£¬
ÓÉÉČŠĪĶ³¼ĘĶ¼æÉµĆ£ŗ”°ĘäĖū”°µÄ°Ł·Ö±ČĪŖ£ŗ![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ21£¬18£¬![]() £»
£»
£Ø3£©![]() £ØČĖ£©£¬
£ØČĖ£©£¬
“š£ŗĻ²»¶”°ĢųÉž”±µÄѧɜČĖŹżĪŖ324ČĖ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijהլŠ”ĒųČēĶ¼ĖłŹ¾£¬Š”Ēų¶«Ī÷Į½¶ĖµÄĀ„![]() ”¢
”¢![]() Ö®¼äµÄ¾ąĄėĪŖ
Ö®¼äµÄ¾ąĄėĪŖ![]() £¬Ä³æŖ·¢ÉĢ×¼±øŌŚĪ»ÓŚ
£¬Ä³æŖ·¢ÉĢ×¼±øŌŚĪ»ÓŚ![]() Ā„µÄ±±Ę«¶«
Ā„µÄ±±Ę«¶«![]() ·½Ļņ£¬ĒŅŌŚ
·½Ļņ£¬ĒŅŌŚ![]() Ā„µÄ±±Ę«Ī÷
Ā„µÄ±±Ę«Ī÷![]() ·½ĻņÉĻµÄ
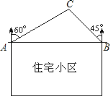
·½ĻņÉĻµÄ![]() “¦øĒŅ»øöÉĢŅµ“óĻĆ£¬Čē¹ūŹ©¹¤ĘŚ¼ä£¬²śÉśµÄŌėŅō»įÓ°Ļģµ½·½Ō²
“¦øĒŅ»øöÉĢŅµ“óĻĆ£¬Čē¹ūŹ©¹¤ĘŚ¼ä£¬²śÉśµÄŌėŅō»įÓ°Ļģµ½·½Ō²![]() “¦£®ĒėÄćĶعż¼ĘĖćĖµĆ÷×”Õ¬Š”ĒųŹĒ·ń»įӊה»§ŹÜµ½ŌėŅōµÄÓ°Ļģ£®£Ø²Īæ¼Źż¾Ż
“¦£®ĒėÄćĶعż¼ĘĖćĖµĆ÷×”Õ¬Š”ĒųŹĒ·ń»įӊה»§ŹÜµ½ŌėŅōµÄÓ°Ļģ£®£Ø²Īæ¼Źż¾Ż![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
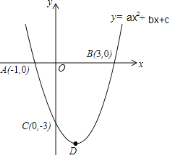
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() £¬
£¬![]() Į½µć£¬Óė
Į½µć£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬µć
£¬µć![]() ŗĶµć
ŗĶµć![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() £¬Å×ĪļĻߵĶŌ³ĘÖįĪŖ
£¬Å×ĪļĻߵĶŌ³ĘÖįĪŖ![]() £¬
£¬![]() ĪŖÅ×ĪļĻߵĶ„µć£®
ĪŖÅ×ĪļĻߵĶ„µć£®
![]() ĒóÅ×ĪļĻߵĽāĪöŹ½£®
ĒóÅ×ĪļĻߵĽāĪöŹ½£®
![]() Å×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µć
Å×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µć![]() £¬Ź¹
£¬Ź¹![]() ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Š“³öµć
ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬Š“³öµć![]() µćµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
µćµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
![]() µć
µć![]() ĪŖĻ߶Ī
ĪŖĻ߶Ī![]() ÉĻŅ»¶Æµć£¬¹żµć
ÉĻŅ»¶Æµć£¬¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļߣ¬ÓėÅ×ĪļĻß½»ÓŚµć
ÖįµÄ“¹Ļߣ¬ÓėÅ×ĪļĻß½»ÓŚµć![]() £¬ĒóĖıߊĪ
£¬ĒóĖıߊĪ![]() Ć껿µÄ×ī“óÖµ£¬ŅŌ¼°“ĖŹ±µć
Ć껿µÄ×ī“óÖµ£¬ŅŌ¼°“ĖŹ±µć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
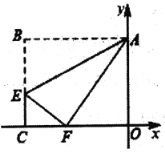
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬³¤·½ŠĪ![]() µÄ±ß
µÄ±ß![]() £¬
£¬![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() Öį£¬
Öį£¬![]() ÖįÉĻ£¬µć
ÖįÉĻ£¬µć![]() ŌŚ±ß
ŌŚ±ß![]() ÉĻ£¬½«øĆ³¤·½ŠĪŃŲ
ÉĻ£¬½«øĆ³¤·½ŠĪŃŲ![]() ÕŪµž£¬µć
ÕŪµž£¬µć![]() Ē”ŗĆĀäŌŚ±ß
Ē”ŗĆĀäŌŚ±ß![]() ÉĻµÄµć
ÉĻµÄµć![]() “¦£¬Čō
“¦£¬Čō![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() ĖłŌŚÖ±Ļߵıķ“ļŹ½ĪŖ__________£®
ĖłŌŚÖ±Ļߵıķ“ļŹ½ĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·“±ČĄżŗÆŹży=![]() £Øk£¾0£©Óė¾ŲŠĪOABCŌŚµŚŅ»ĻóĻŽĻą½»ÓŚD”¢EĮ½µć£¬OA=2£¬OC=4£¬Į¬½ÓOD”¢OE”¢DE.¼Ē”÷OAD”¢”÷OCEµÄĆ껿·Ö±šĪŖS”¢S .
£Øk£¾0£©Óė¾ŲŠĪOABCŌŚµŚŅ»ĻóĻŽĻą½»ÓŚD”¢EĮ½µć£¬OA=2£¬OC=4£¬Į¬½ÓOD”¢OE”¢DE.¼Ē”÷OAD”¢”÷OCEµÄĆ껿·Ö±šĪŖS”¢S .
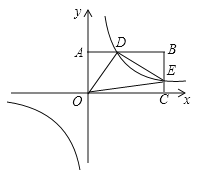
£Ø1£©¢ŁµćBµÄ×ų±źĪŖ £»¢ŚS S£ØĢī”°£¾”±”¢”°£¼”±”¢”°=”±£©£»
£Ø2£©µ±µćDĪŖĻ߶ĪABµÄÖŠµćŹ±£¬ĒókµÄÖµ¼°µćEµÄ×ų±ź£»
£Ø3£©µ±S+S=2Ź±£¬ŹŌÅŠ¶Ļ”÷ODEµÄŠĪד£¬²¢Ēó”÷ODEµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
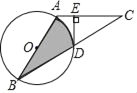
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬CŹĒ”ŃOĶāŅ»µć£¬AB=AC£¬Į¬½ÓBC£¬½»”ŃOÓŚµćD£¬¹żµćD×÷DE”ĶAC£¬“¹×ćĪŖE£®
(1)ĒóÖ¤£ŗDEÓė”ŃOĻąĒŠ£®
(2)Čō”ĻB=30”ć£¬AB=4£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ŹĒ”” ””£Ø½į¹ū±£ĮōøłŗÅŗĶ¦Š£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=©x+2Óė·“±ČĄżŗÆŹży=![]() £Øk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Øa£¬3£©£¬B£Ø3£¬b£©Į½µć£¬¹żµćA×÷AC”ĶxÖįÓŚµćC£¬¹żµćB×÷BD”ĶxÖįÓŚµćD£®
£Øk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Øa£¬3£©£¬B£Ø3£¬b£©Į½µć£¬¹żµćA×÷AC”ĶxÖįÓŚµćC£¬¹żµćB×÷BD”ĶxÖįÓŚµćD£®
(1)Ēóa£¬bµÄÖµ¼°·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
(2)ČōµćPŌŚÖ±Ļßy=©x+2ÉĻ£¬ĒŅS”÷ACP=S”÷BDP£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»
(3)ŌŚxÖįÕż°ėÖįÉĻŹĒ·ń“ęŌŚµćM£¬Ź¹µĆ”÷MABĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öMµćµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÕż±ČĄżŗÆŹżŗĶ·“±ČĄżŗÆŹżµÄĶ¼Ļ󶼾¹żµćA£Ø©3£¬©3£©£®
£Ø1£©ĒóÕż±ČĄżŗÆŹżŗĶ·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©°ŃÖ±ĻßOAĻņÉĻĘ½ŅĘŗóÓė·“±ČĄżŗÆŹżµÄĶ¼Ļó½»ÓŚµćB£Ø©6£¬m£©£¬ÓėxÖį½»ÓŚµćC£¬ĒómµÄÖµŗĶÖ±ĻßBCµÄ±ķ“ļŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Ö±ĻßBCÓėyÖį½»ÓŚµćD£¬ĒóŅŌµćA£¬B£¬DĪŖ¶„µćµÄČż½ĒŠĪµÄĆ껿£»
£Ø4£©ŌŚ£Ø3£©µÄĢõ¼žĻĀ£¬µćA£¬B£¬DŌŚ¶ž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬ŹŌÅŠ¶Ļøƶž“ĪŗÆŹżŌŚµŚČżĻóĻŽÄŚµÄĶ¼ĻóÉĻŹĒ·ń“ęŌŚŅ»µćE£¬Ź¹ĖıߊĪOECDµÄĆ껿S1ÓėĖıߊĪOABDµÄĆ껿SĀś×ć£ŗS1=![]() S£æČō“ęŌŚ£¬ĒóµćEµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
S£æČō“ęŌŚ£¬ĒóµćEµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com