
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBгвВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBгвВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
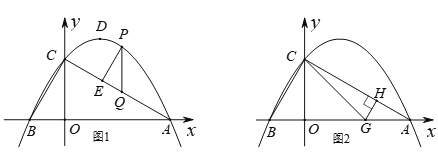
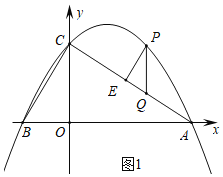
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгACЁЂBCЃЌШєЕуPЪЧжБЯпACЩЯЗНХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPE//BCНЛ![]() гкЕуEЃЌзїPQ//yжсНЛACгкЕуQЃЌЕБЁїPQEжмГЄзюДѓЪБЃЌШєЕуMдкyжсЩЯЃЌЕуNдкxжсЩЯЃЌЧѓPM+MN
гкЕуEЃЌзїPQ//yжсНЛACгкЕуQЃЌЕБЁїPQEжмГЄзюДѓЪБЃЌШєЕуMдкyжсЩЯЃЌЕуNдкxжсЩЯЃЌЧѓPM+MN![]() ANЕФзюаЁжЕЃЛ
ANЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуGЮЊxжсе§АыжсЩЯвЛЕуЃЌЧвOG=OCЃЌСЌНгCGЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌМЧа§зЊжаЕФ
ЃЌМЧа§зЊжаЕФ![]() ЮЊЁї
ЮЊЁї![]() ЃЌдка§зЊЙ§ГЬжаЃЌжБЯп
ЃЌдка§зЊЙ§ГЬжаЃЌжБЯп![]() ЃЌ
ЃЌ![]() ЗжБ№гыжБЯп
ЗжБ№гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌЁї
ЃЌЁї![]() ФмЗёГЩЮЊЕШбќШ§НЧаЮЃПШєФмЧыжБНгаДГіЫљгаТњзуЬѕМўЕФ
ФмЗёГЩЮЊЕШбќШ§НЧаЮЃПШєФмЧыжБНгаДГіЫљгаТњзуЬѕМўЕФ![]() ЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉPM+MNЉ![]() ANЕФзюаЁжЕЪЧ
ANЕФзюаЁжЕЪЧ![]() ЃЛЃЈ2ЃЉТњзуЬѕМўЕФа§зЊНЧІСЮЊ15ЁуЛђ37.5ЁуЛђ60ЁуЛђ127.5ЁуЃЎ
ЃЛЃЈ2ЃЉТњзуЬѕМўЕФа§зЊНЧІСЮЊ15ЁуЛђ37.5ЁуЛђ60ЁуЛђ127.5ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙЙНЈЖўДЮКЏЪ§ЃЌЧѓГіЕуPзјБъЃЌШчЭМ2жаЃЌзїsinЁЯOAF=![]() , зїPNЁЭAFЃЌдђгаPM+MNЁнPNЃЌNH=
, зїPNЁЭAFЃЌдђгаPM+MNЁнPNЃЌNH=![]() ANЃЌПЩжЊPM+MN-AN
ANЃЌПЩжЊPM+MN-AN![]() ANЕФзюаЁжЕМДЮЊPHЕФГЄЃЌИљОнЭЌНЧЕФШ§НЧКЏЪ§ПЩЕУPHЕФГЄЃЛ
ANЕФзюаЁжЕМДЮЊPHЕФГЄЃЌИљОнЭЌНЧЕФШ§НЧКЏЪ§ПЩЕУPHЕФГЄЃЛ
ЃЈ2ЃЉЗжЫФжжЧщаЮЗжБ№ЛГіЭМаЮЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЛ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЖдгкХзЮяЯп![]() ,Сюy=0ЃЌЕУЕНx=6Лђ-2ЃЌ
,Сюy=0ЃЌЕУЕНx=6Лђ-2ЃЌ
ЁрAЃЈ6ЃЌ0ЃЉЃЌBЃЈ-2ЃЌ0ЃЉЃЌ
ЕБx=0ЪБЃЌy=2![]() ,
,
ЁрCЃЈ0ЃЌ2![]() ЃЉ,
ЃЉ,
RtЁїAOCжаЃЌOC=2![]() , OA=6,
, OA=6,
ЁрAC=4![]() ,
,
ЁрЁЯACO=60ЁуЃЌЭЌРэЕУЁЯBCO=30Ёу
ЁрЁЯACB=30Ёу+60Ёу=90ЁуЃЌ
ЁпPEЁЮBCЃЌ
ЁрЁЯPEQ=90ЁуЃЌ
ЁпPQЁЮyжсЃЌ
ЁрЁЯACO=ЁЯPQC=60ЁуЃЌ
ЁрЕБPQзюДѓЪБЃЌЁїPQEжмГЄзюДѓЃЌ
![]()
Щш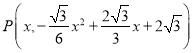 ЃЌдђ
ЃЌдђ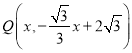 ЃЌ
ЃЌ
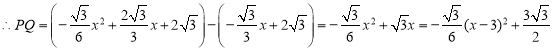
ЕБx=3ЪБЃЌPQзюГЄЃЌДЫЪБЃЌЁїPQEжмГЄзюДѓЃЌ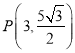
ШчЭМ2ЃЌдкyжсЩЯШЁЕу![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
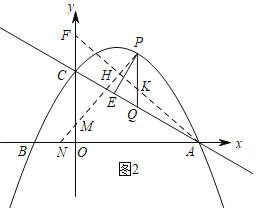
![]() ЃЌзїPHЁЭAFЃЌНЛAFгкHЃЌНЛyжсгкMЃЌНЛxжсгкNЃЌAFНЛPQгкKЃЌ
ЃЌзїPHЁЭAFЃЌНЛAFгкHЃЌНЛyжсгкMЃЌНЛxжсгкNЃЌAFНЛPQгкKЃЌ
![]()
![]()
дђPM+MN-AN![]() ANЕФзюаЁжЕМДЮЊPHЕФГЄЃЌ
ANЕФзюаЁжЕМДЮЊPHЕФГЄЃЌ
ЁпAЃЈ6ЃЌ0ЃЉЃЌ![]() ЃЌ
ЃЌ
взЕУжБЯпAFЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЕБx=3ЪБЃЌ![]()
![]()
![]()
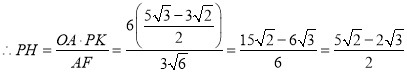
злЩЯЃЌPM+MN-AN![]() ANЕФзюаЁжЕЪЧ
ANЕФзюаЁжЕЪЧ![]() .
.
ЃЈ2ЃЉШчЭМ3жаЃЌЕБMN=MGЁфЪБЃЌЩшOAНЛGЁфNгкLЃЌ
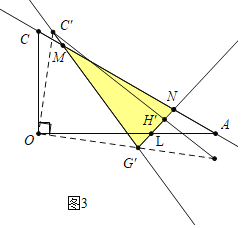
ЁпЁЯMGЁфN=75ЁуЃЌ
ЁрЁЯMNGЁф=ЁЯMGЁфN=75ЁуЃЌ
ЁрЁЯNLA=75Ёу-30Ёу=45ЁуЃЌ
ЁпЁЯOLG'=ЁЯNLA=45ЁуЃЌЁЯOGЁфL=45Ёу+75Ёу=120ЁуЃЌ
ЁрЁЯAOGЁф=180Ёу-120Ёу-45Ёу=15ЁуЃЌ
Ёра§зЊНЧЮЊ15ЁуЃЎ
ШчЭМ4жаЃЌЕБGЁфM=GЁфNЪБЃЌЩшOAНЛCЁфGЁфгкLЃЎ
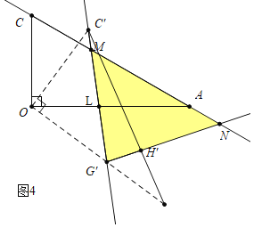
ЁпЁЯMGЁфN=75ЁуЃЌ
ЁрЁЯGЁфMN=![]() ЃЈ180Ёу-75ЁуЃЉ=52.5ЁуЃЌ
ЃЈ180Ёу-75ЁуЃЉ=52.5ЁуЃЌ
ЁрЁЯOLGЁф=ЁЯALM=180Ёу-30Ёу-52.5Ёу=97.5ЁуЃЌ
ЁрЁЯAOGЁф=180Ёу-97.5Ёу-45Ёу=37.5ЁуЃЌ
Ёра§зЊНЧЮЊ37.5ЁуЃЎ
ШчЭМ5жаЃЌЕБNGЁф=NMЪБЃЌЩшOAНЛGЁфCЁфгкLЃЎ

ЁпЁЯNGЁфM=ЁЯNMGЁф=75ЁуЃЌ
ЁрЁЯMNGЁф=ЁЯCAO=30ЁуЃЌ
ЁрALЁЮNGЁфЃЌ
ЁрЁЯOLGЁф=ЁЯMG'N=75ЁуЃЌ
ЁрЁЯAOGЁф=180Ёу-75Ёу-45Ёу=60ЁуЃЌ
Ёра§зЊНЧЮЊ60ЁуЃЎ
ШчЭМ6жаЃЌЕБGЁфM=GЁфNЪБЃЌ
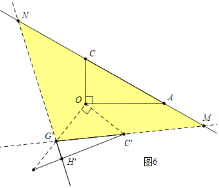
ЁпЁЯMGЁфN=180Ёу-75Ёу=105ЁуЃЌ
ЁрЁЯNMGЁф=![]() ЃЈ180Ёу-105ЁуЃЉ=37.5ЁуЃЌ
ЃЈ180Ёу-105ЁуЃЉ=37.5ЁуЃЌ
ЁрЁЯAOCЁф=360Ёу-150Ёу-135Ёу-37.5Ёу=37.5ЁуЃЌ
ЁрЁЯAOGЁф=90Ёу+37.5Ёу=127.5Ёу
Ёра§зЊНЧЮЊ127.5ЁуЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФа§зЊНЧІСЮЊ15ЁуЛђ37.5ЁуЛђ60ЁуЛђ127.5ЁуЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
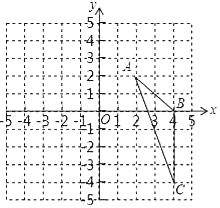
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCШ§ИіЖЅЕуЕФзјБъЗжБ№ЪЧAЃЈ2ЃЌ2ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ4ЃЌЉ4ЃЉЃЎ
ЃЈ1ЃЉЧыдкЭМжаЃЌЛГіЁїABCЯђзѓЦНвЦ6ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉвдЕуOЮЊЮЛЫЦжааФЃЌНЋЁїABCЫѕаЁЮЊдРДЕФ![]() ЃЌЕУЕНЁїA2B2C2ЃЌЧыдкЭМжаyжсгвВрЃЌЛГіЁїA2B2C2ЃЌВЂЧѓГіЁЯA2C2B2ЕФе§ЯвжЕЃЎ
ЃЌЕУЕНЁїA2B2C2ЃЌЧыдкЭМжаyжсгвВрЃЌЛГіЁїA2B2C2ЃЌВЂЧѓГіЁЯA2C2B2ЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтОХФъМЖбЇЩњЬхг§ВтЪдГЩМЈЧщПіЃЌвдОХФъМЖЃЈ1ЃЉАрбЇЩњЕФЬхг§ВтЪдГЩМЈЮЊбљБОЃЌАДBЁЂCЁЂDЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦШчЯТСНЗљЭГМЦЭМЃЌЧыФуНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃКЃЈЫЕУїЃКAМЖЃК90ЗжЉ100ЗжЃЛBМЖЃК75ЗжЉ89ЗжЃЛCМЖЃК60ЗжЁЋ74ЗжЃЛDМЖЃК60ЗжвдЯТЃЉ
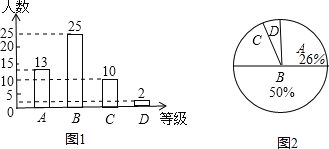
ЃЈ1ЃЉЧѓГіDМЖбЇЩњЕФШЫЪ§еМШЋАрзмШЫЪ§ЕФАйЗжБШЃЛ
ЃЈ2ЃЉЧѓГіЩШаЮЭГМЦЭМЃЈЭМ2ЃЉжаCМЖЫљдкЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєИУаЃОХФъМЖбЇЩњЙВга500ШЫЃЌЧыФуЙРМЦетДЮПМЪджаAМЖКЭBМЖЕФбЇЩњЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТл: Ђй abcЃМ0ЃЛЂк 2aЃЋbЃН0; Ђл b2Ѓ4acЃМ0ЃЛЂм 9a+3b+cЃО0; Ђн c+8aЃМ0.е§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ.
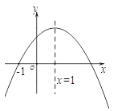
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪпВЫЛљЕиЮЊбЁГіЪЪгІЪаГЁашЧѓЕФЮїКьЪСбэУчЃЌдкЬѕМўЛљБОЯрЭЌЕФЧщПіЯТЃЌНЋМзЁЂввСНИіЦЗжжЕФЮїКьЪСбэУчИї500жъжжжВдкЭЌвЛИіДѓХяЃЎЖдЪаГЁзюЮЊЙизЂЕФВњСПНјааСЫГщбљЕїВщЃЌЫцЛњДгМзЁЂввСНИіЦЗжжЕФЮїКьЪСбэУчжаИїЪеМЏСЫ50жъбэУчЩЯЕФЙвЙћЪ§ЃЈЮїКьЪСЕФИіЪ§ЃЉЃЌВЂЖдЪ§ОнЃЈИіЪ§ЃЉНјааећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂ.
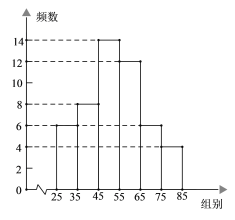
a. МзЦЗжжЙвЙћЪ§ЦЕЪ§ЗжВМжБЗНЭМЃЈЪ§ОнЗжГЩ6зщЃК25Ёмx<35ЃЌ35Ёмx<45ЃЌ45Ёмx<55ЃЌ55Ёмx<65ЃЌ65Ёмx<75ЃЌ75Ёмx<85ЃЉ.
b. МзЦЗжжЙвЙћЪ§дк45Ёмx<55етвЛзщЕФЪЧЃК
45ЃЌ45ЃЌ46ЃЌ47ЃЌ47ЃЌ49ЃЌ49ЃЌ49ЃЌ49ЃЌ50ЃЌ50ЃЌ51ЃЌ51ЃЌ54
c. МзЁЂввЦЗжжЙвЙћЪ§ЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
ЦЗжж | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю |
Мз | 49.4 | m | 49 | 1944.2 |
вв | 48.6 | 48.5 | 47 | 3047 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬт:
(1)Бэжаm= ЃЛ
(2)ЪдЙРМЦМзЦЗжжЙвЙћЪ§ГЌЙ§49ИіЕФЮїКьЪСбэУчЕФЪ§СПЃЛ
(3)ПЩвдЭЦЖЯГі ЦЗжжЕФЮїКьЪСбэУчИќЪЪгІЪаГЁашЧѓЃЌРэгЩЮЊ ЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
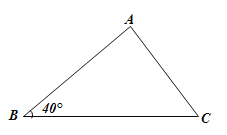
ЁОЬтФПЁПдкжБНЧШ§НЧаЮжаЃЌШчЙћвбжЊ2ИідЊЫиЃЈЦфжажСЩйгавЛИіЪЧБпЃЉЃЌФЧУДОЭПЩвдЧѓГіЦфгрЕФ3ИіЮДжЊдЊЫиЃЎЖдгкШЮвтШ§НЧаЮЃЌЮвУЧашвЊжЊЕРМИИідЊЫиОЭПЩвдЧѓГіЦфгрЕФЮДжЊдЊЫиФиЃПЫМПМВЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЙлВьЯТСа4ЗљЭМЃЌИљОнЭМжавбжЊдЊЫиЃЌПЩвдЧѓГіЦфгрЮДжЊдЊЫиЕФШ§НЧаЮЪЧ ЃЎ
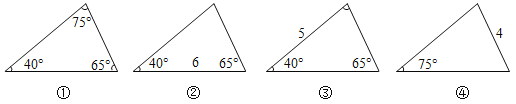
ЃЈ2ЃЉШчЭМЃЌдкЁїABCжаЃЌвбжЊЁЯBЃН40ЁуЃЌBCЃН18ЃЌABЃН15ЃЌЧыЧѓГіACЕФГЄЖШЃЈД№АИБЃСєИљКХЃЉЃЎЃЈВЮПМЪ§ОнЃКsin40ЁуЁж0.6ЃЌcos40ЁуЁж0.8ЃЌtan40ЁуЁж0.75ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
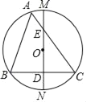
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌABЃНBCЃЌжБОЖMNЁЭBCгкЕуDЃЌгыACБпЯрНЛгкЕуEЃЌШєЁбOЕФАыОЖЮЊ2![]() ЃЌOEЃН2ЃЌдђODЕФГЄЮЊ_____ЃЎ
ЃЌOEЃН2ЃЌдђODЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ

ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃаЫШЄаЁзщОЭЁАзюЯыШЅЕФеФжн5ИізюУРЯчДхЁБЫцЛњЕїВщСЫБОаЃВПЗжбЇЩњ. вЊЧѓУПЮЛЭЌбЇбЁдёЧвжЛФмбЁдёвЛИізюЯыШЅЕФзюУРЯчДх. ЯТУцЪЧИљОнЕїВщНсЙћЛцжЦГіЕФЩаВЛЭъећЭГМЦБэКЭЭГМЦЭМЃЌЦфжаxЁЂyЪЧТњзуx<yЕФе§ећЪ§.
зюУРЯчДхвтЯђЭГМЦБэ
зюУРЯчДх | ШЫЪ§ |
AЃКСњКЃмЄУРДх | 10 |
BЃКЛЊАВЙйЎДх | 11 |
CЃКГЄЬЉЩНжиДх | 4x |
DЃКФЯОИЫўЯТДх | 9 |
EЃКЖЋЩНАФНЧДх | 3y |
зюУРЯчДхвтЯђЩШаЮЭГМЦЭМ
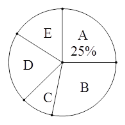
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
(1)ЧѓxЁЂyЕФжЕЃЛ
(2)ШєИУаЃга1200УћбЇЩњЃЌЧыЙРМЦЁАзюЯыШЅЛЊАВЙйЎДхЁБЕФбЇЩњШЫЪ§.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com