
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价![]() (万元)之间满足关系式
(万元)之间满足关系式![]() ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本![]() (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.

(1)求月产量x的范围;
(2)如果想要每月利润为1750万元,那么当月产量应为多少套?
(3)如果每月获利润不低于1900万元,当月产量x(套)为多少时,生产总成本最低?并求出此时的最低成本.
【答案】(1)25≤x≤40;(2)x=25;(3)当x=30时,成本最低,最低成本为1400万元.
【解析】(1)根据题中条件“每套产品的生产成本不高于50万元,每套产品的售价不低于90万元”列出不等式组求解月产量x的范围;(2)根据利润=售价-成本列出关系式,进而解答即可.(3)得出函数关系式,然后根据二次函数的最大值及最小值可确定答案.
本题解析:
(1)设函数关系式为y2=kx+b,把坐标(30,1400)(40,1700)代入,
得![]() ,解得:
,解得: ![]() ,
,
∴函数关系式y2=30x+500,由![]() ,解得:25≤x≤40;
,解得:25≤x≤40;
(2)1750=y1-y2 (170-2x)x-(30x+500)=1750 ∴x1=45 x2=25 ∵25≤x≤40 ∴x=25
(3)当x=30时,成本最低,最低成本为1400万元


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( ) 
A.10
B.12
C.16
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为_____________
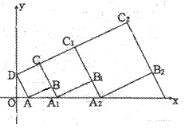
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 两条直线被第三条直线所截,同位角相等B. 垂直于同一直线的两直线平行
C. 相等的角是对顶角D. 平行于同一直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图甲,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形. 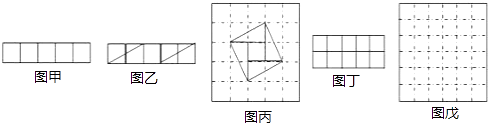
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x= ![]() 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的小正方形,排列形式如图丁,请把它们分割后拼接成一个新的正方形.要求:在图丁中画出分割线,并在图戊的正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
说明:直接画出图形,不要求写分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,有题译文如下:今有门,不知其高宽;有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线长恰好相等.问门高、宽和对角线的长各是多少?设门对角线的长为x尺,下列方程符合题意的是( )
A.(x+2)2+(x-4)2=x2B.(x-2)2+(x-4)2=x2
C.x2+(x-4)2=(x-4)2D.(x-2)2+x2=(x+4)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com