
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.
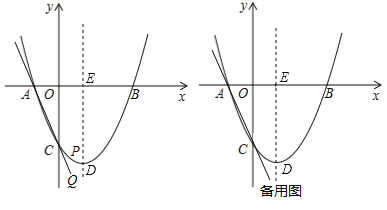
(1)求抛物线的解析式;
(2)点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.
①求线段PQ的长度n关于m的函数关系式;
②连接AP,CP,求当△ACP面积为![]() 时点P的坐标;
时点P的坐标;
(3)若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)①n=m2+m;②P(![]() ,﹣
,﹣![]() );(3)存在,BN=2
);(3)存在,BN=2![]() 或2或2
或2或2![]()
【解析】
(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,即可求解;
(2)①AC的表达式为:y=﹣3x﹣3,则点Q(m,﹣3m﹣3),n=PQ=m2﹣2m﹣3+3m+3=m2+m;△ACP面积=![]() ×CH×(xP﹣xA)=
×CH×(xP﹣xA)=![]() m(m+1)=
m(m+1)=![]() ,即可求解;
,即可求解;
(3)分BC是边、BC是对角线两种情况,分别求解即可.
(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)设点P(m,m2﹣2m﹣3),
①将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣3x﹣3,则点Q(m,﹣3m﹣3),
n=PQ=m2﹣2m﹣3+3m+3=m2+m;
②连接AP交y轴于点H,
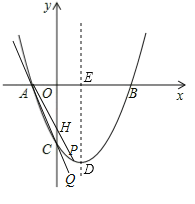
同理可得:直线AP的表达式为:y=(m﹣3)x+m﹣3,
则OH=3﹣m,则CH=m,
△ACP面积=![]() ×CH×(xP﹣xA)=
×CH×(xP﹣xA)=![]() m(m+1)=
m(m+1)=![]() ,
,
解得:m=![]() (不合题意的值已舍去),
(不合题意的值已舍去),
故点P(![]() ,﹣
,﹣![]() );
);
(3)点C(0,﹣3),点B(3,0),设点P(m,n),n=m2﹣2m﹣3,点N(1,s),
①当BC是边时,
点C向右平移3个单位向上平移3个单位得到B,
同样点M(N)向右平移3个单位向上平移3个单位得到N(M),
即1±3=m,s±3=n,
解得:m=4或﹣2,s=2或0,
故点N(1,2)或(1,0),则BN=2![]() 或2;
或2;
②当BC是对角线时,
由中点公式得:3=m+1,3=s+n,
解得:s=6,故点N(1,6),则BN=2![]() ,
,
综上,BN=2![]() 或2或2
或2或2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小亮利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是他剪裁出的空心等边三角形、正方形、矩形、正五边形,若每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A. B.
B. C.
C. D.
D.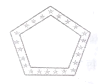
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名场上队员的身高(单位:cm)是:180,182,184,186,190,194.现用一名身高为188cm的队员换下场上身高为182cm的队员,与换人前相比,场上队员的身高
A.平均数变小,方差变小B.平均数变小,方差变大
C.平均数变大,方差变小D.平均数变大,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
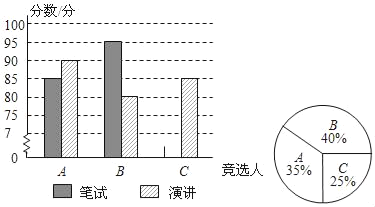
【题目】定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 |
| 80 | 85 |
(1)请将表和图中的空缺部分补充完整;
(2)图中B同学对应的扇形圆心角为 度;
(3)竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为 ,B同学得票数为 ,C同学得票数为 ;
(4)若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断 当选.(从A、B、C、选择一个填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,我们规定:一个锐角的对边与斜边的比值称为这个锐角的正弦值.
例如:Rt△ABC中,∠C=90°,∠A的对边BC与斜边AB的比值,即![]() 就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:60°的正弦值约在0.85~0.88之间取值,45°的正弦值约在0.70~0.72之间取值.下列角度中正弦值最接近0.94的是( )
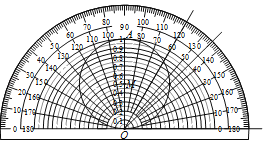
A.30°B.50°C.40°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() 与
与![]() 轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2.
轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2.
(1)求b的值;
(2)求抛物线y2的表达式;
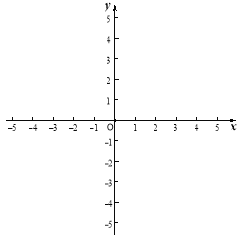
(3)抛物线y2与![]() 轴交于点D,与
轴交于点D,与![]() 轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线
轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线![]() 与图象G有一个公共点,请结合函数图象,求直线
与图象G有一个公共点,请结合函数图象,求直线![]() 与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校选学生会正副主席,需要从甲班的2名男生1名女生(男生用A,B表示,女生用a表示)和乙班的1名男生1名女生(男生用C表示,女生用b表示)共5人中随机选出2名同学.
(1)用树状图或列表法列出所有可能情形;
(2)求2名同学来自不同班级的概率;
(3)求2名同学恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点H,E在BC边上,点G,F在CD边上,连接AF,AG,AE,HF,AG垂直平分CF,HF分别交AE,AG于点M,N,∠AEB=45°,∠FHC=∠GAE.
(1)若AF=![]() ,tan∠FAG=
,tan∠FAG=![]() ,求AN;
,求AN;
(2)若∠FHC=2∠FAG,求证:![]() AE=MN+BE.
AE=MN+BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com