
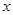 的一元二次方程
的一元二次方程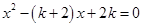 .
.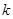 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;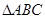 的一边
的一边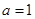 ,若另两边
,若另两边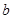 、
、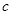 恰好是这个方程的两个根,求
恰好是这个方程的两个根,求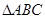 的周长.
的周长.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
|
|
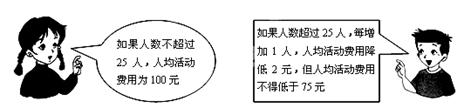 春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
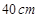 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.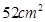 ,小林该怎么剪?
,小林该怎么剪?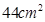 .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
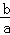 ,x1•x2=
,x1•x2=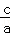 .根据该材料填空:已知x1,x2,是方程x2+6x+3=0的两实数根,则
.根据该材料填空:已知x1,x2,是方程x2+6x+3=0的两实数根,则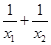 的值为 _________ .
的值为 _________ .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
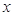 | 3.24 | 3.25 | 3.26 |
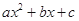 | -0.02 | 0.01 | 0.03 |
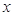 的方程
的方程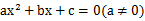 的一个解
的一个解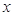 的范围是( )
的范围是( )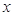 <3.24 B.3.24<
<3.24 B.3.24<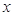 <3.25
<3.25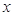 <3.26 D.
<3.26 D.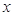 >3.25
>3.25查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com