
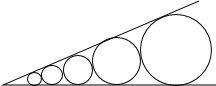
 如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切,且半径分别为r1、r2、r3、r4、r5.若最小的半径r1=1,最大的半径r5=81.则sinθ=$\frac{\sqrt{3}}{2}$.
如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切,且半径分别为r1、r2、r3、r4、r5.若最小的半径r1=1,最大的半径r5=81.则sinθ=$\frac{\sqrt{3}}{2}$. 分析 连接O1M,O2N,根据切线的性质可得O1M⊥OA,O2N⊥OA,根据切线长定理可得∠AOO1=∠BOO1=$\frac{1}{2}$θ,过点O1作O1H⊥O2N于H,易证四边形O1MNH是平行四边形,∠HO1O2=∠AOO1=$\frac{1}{2}$θ,根据外切两圆的性质可得O1O2=r1+r2.在Rt△O1HO2中运用三角函数可求出$\frac{{r}_{2}}{{r}_{1}}$(用sin$\frac{1}{2}θ$的式子表示),同理可求出$\frac{{r}_{5}}{{r}_{4}}$、$\frac{{r}_{4}}{{r}_{3}}$、$\frac{{r}_{3}}{{r}_{2}}$,然后根据r1=1,r5=81可求出θ,就可解决问题.
解答 解: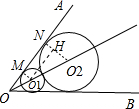 连接O1M,O2N,如图,
连接O1M,O2N,如图,
则有O1M⊥OA,O2N⊥OA,∠AOO1=∠BOO1=$\frac{1}{2}$∠AOB=$\frac{1}{2}$θ,
∴O1M∥O2N.
过点O1作O1H⊥O2N于H,
则有O1H∥OA,
∴四边形O1MNH是平行四边形,∠HO1O2=∠AOO1=$\frac{1}{2}$θ,
∴NH=MO1=r1,O2H=r2-r1.
∵⊙O1与⊙O2外切,
∴O1O2=r1+r2.
在Rt△O1HO2中,
sin∠HO1O2=$\frac{O2H}{O1O2}$=$\frac{{r}_{2}-{r}_{1}}{{r}_{1}+{r}_{2}}$=sin$\frac{1}{2}$θ,
∴$\frac{{r}_{2}}{{r}_{1}}$=$\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$.
同理:$\frac{{r}_{3}}{{r}_{2}}$=$\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$,$\frac{{r}_{4}}{{r}_{3}}$=$\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$,$\frac{{r}_{5}}{{r}_{4}}$=$\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$,
∴$\frac{{r}_{5}}{{r}_{1}}$=$\frac{{r}_{5}}{{r}_{4}}$•$\frac{{r}_{4}}{{r}_{3}}$•$\frac{{r}_{3}}{{r}_{2}}$•$\frac{{r}_{2}}{{r}_{1}}$=($\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$)4=$\frac{81}{1}$=81,
∴$\frac{1+sin\frac{1}{2}θ}{1-sin\frac{1}{2}θ}$=3(舍负),
∴sin$\frac{1}{2}$θ=$\frac{1}{2}$,
∴$\frac{1}{2}$θ=30°,
∴θ=60°,
∴sinθ=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了两圆外切的性质、圆的切线的性质、平行四边形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,有一定的难度,求出相邻两圆半径之间的比是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
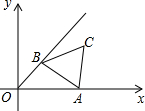 如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{3}$ | D. | 1+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 银行存款500元,一年后可得利息171元 | |
| B. | 甲比乙重3kg,乙比甲小一岁 | |
| C. | 两班排球比赛,打满5局,甲班胜两局,乙班胜三局 | |
| D. | 两次测验,第一次得80分,第二次比第一次高6分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
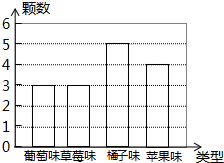 小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )
小林给弟弟买了一些糖果,放到一个不透明的袋子里,这些糖果除了口味和外包装的颜色外其余都相同,袋子里各种口味糖果的数量统计如图所示,他让弟弟从袋子里随机摸出一颗糖果.则弟弟恰好摸到橘子味糖果的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com