练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

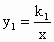    已知反比例函数和一次函数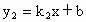，当x=4时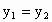，；当x=2时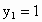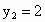，，，求这两个函数的关系式．

    答案：略
    解析：

    解：由题意知，解得．

    所以，．


    提示：

    根据条件，当x=4时，，，而，所以①，当x=2时，②，③．先解②得，然后代入①，联立③得到关于和b的方程组，解得，b．从而得到这两个函数的关系式．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    某名牌洁具厂生产的一款经典淋浴花洒A（简称“花洒A”），因其造型时尚典雅，质量过硬，在市场上供不应求，深受消费者喜爱．但花洒的价格受其主要原材料铜的价格的影响很大，从去年1至12月，国内铜价一路下跌，每千克铜价y（元）与月份x（1≤x≤12，且x取正整数）之间的函数关系如下表：
    月份x 1 2 3 4 5 6 7 8 9 10 11 12
    铜价y（元/千克） 59 58 57 56 55 54 53 52 51 50 49 48
    该洁具厂每月按定单数量购买原材料组织生产，并将每套花洒A的出厂价定为680元．已知每套花洒A的含铜量为8千克，每套花洒A的其它成本为120元，且1至12月花洒A的定单数量p（万套）与月份x满足函数关系式p=-0.1x+2.2（1≤x≤12，且x取正整数）．
    （1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求出y与x之间的函数关系式；
    （2）求该厂去年生产花洒A的利润W（万元）与x（月）之间的函数关系式，并求出哪个月生产花洒A的利润最大，且最大利润是多少万元？
    （3）受国际大宗商品价格上涨的影响，今年1月的铜价比去年12月每千克上涨10元，另一方面，由于临近春节原材料成本增长，其它成本上涨至131元/套．该洁具厂决定从今年1月开始，每套花洒A的出厂价在去年的基础上提高a%，与此同时花洒A的月定单数量在去年12月的基础上减少1.8a%．但是，为解决0.8万个水龙头B的库存问题，洁具厂计划今年1月在原定单基础上多生产0.8万套花洒A，与水龙头B搭配成淋浴组合C（一套花洒A+1个水龙头B）进行销售，已知每年个水龙头B的所有成本是105元（含铜成本），洁具厂将每套淋浴组合C的出厂价定为1000元，新增的0.8万套淋浴组合C定单被抢购一空．这样，该厂今年1月计划生产的花洒A和淋浴组合C获总利润376万元．请你参考以下数据，估算出a的整数值（0＜a＜20）．
    （参考数据：9.62=92.16，9.72=94.09，9.82=96.04，9.92=98.01）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

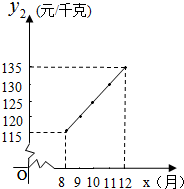    某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价y1与月份x（1≤x≤7，且x为整数），之间的函数关系式如下表：
    月份x 1 2 3 4 5 6 7
    y1（元/千克） 50 60 70 80 90 100 110
    随着我国对一些国家进出口关税的调整，该水果的进价涨势趋缓，在8至12月份每千克水果A的进价y2与月份x（8≤x≤12，且x为整数）之间存在如下图所示的变化趋势．
    （1）请观察表格和图象，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出y1与x和y2与x的函数关系式．
    （2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量p1（千克）与月份x满足：p1=10x+80；8月至12月的销量p2（千克）与月份x满足：p2=-10x+250；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润．
    （3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了a%（a＜100），与此同时每月的销量均在去年12月的基础上减少了0.2a%，这样销售下去要使今年1至6月的总利润为68130元，试求出a的值．（保留两个有效数字）（参考数据：232=529，242=576，252=625，262=676）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

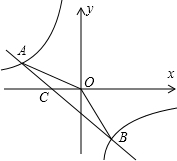    已知点A（-8，n），B（3，-8）是一次函效y=kx+b的图象和反比例函数y=
    m
    x
    图象的两个交点．
    （1）求反比例函数和一次函数的解析式；
    （2）求直线AB与x轴的交点C的坐标及△AOB的面积；
    （3）求不等式kx+b-
    m
    x
    ＞0    的解集（请直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    2011年5月9日，我市成立了首支食品药品犯罪侦缉支队，专门打击危害食品药品安全的违法犯罪行为，食品安全已越来越受到人们的关注．我市某食品加工企业严把质量关，积极生产“绿色健康”食品，由于受食品原料供应等因素的影响，生产“绿色健康”食品的产量随月份增加呈下降趋势．今年前5个月生产的“绿色健康”食品y（吨）与月份（x）之间的关系如下表：
    月份x（月） 1 2 3 4 5 …
    “绿色健康”食品产量y（吨） 48 46 44 42 40 …
    （1）请你从学过的一次函数、二次函数、反比例函数确定哪种函数关系能表示出y与x的变化规律，并求出y与x的函数关系式．
    （2）随着“绿色健康”食品生产量的减少，每生产一吨“绿色健康”食品，企业相应获得的利润有所提高，且每生产一吨获得的利润P（百元）与月份x（月）成一次函数关系．已知1月份每生产一吨“绿色健康”食品，企业相应获利80百元，4月份每生产一吨“绿色健康”食品企业相应获利95百元．那么今年哪月份该企业获得的利润最大？最大利润是多少百元？
    （3）受国家法律保护的激励，该企业决定今年5月份起，更新食品安全检测设备的同时，扩建食品原料基地以提高生产“绿色健康”食品的产量．更新设备检测费用和扩建原料基地费用共用去4000百元，预计从6月份起，每月生产一吨“绿色健康”食品的产量在上一个月基础上增加a%，与此同时，每生产一吨“绿色健康”食品，企业相应获得的利润在上一个月的基础上增加20%，要使今年6、7月份利润的总和在扣除设备检测费用和扩建基地费用后，仍是今年5月份月利润的2倍，求a的整数值．（参考数据：
    		11
    ≈3.317    ，
    		12
    ≈3.464    ，
    		13
    ≈3.606    ，
    		14
    ≈3.742    ）

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（山东莱芜卷）数学 题型：解答题

    （本小题满分12分）已知反比例函数和一次函数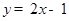，其中一次

    函数图象经过（a，b）与（a+1，b+k）两点.

    (1) 求反比例函数的解析式．

    (2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.

    (3) 利用(2)的结果,请问:在X轴上是否存在点P，使△AOP为等腰三角形?若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案