
分析 首先求出方程$\frac{mx}{x-3}$-2=$\frac{1-x}{3-x}$的解是多少,然后根据方程的解为正数,求出m的取值范围即可.
解答 解:∵$\frac{mx}{x-3}$-2=$\frac{1-x}{3-x}$,
∴mx-2(x-3)=x-1,
∴x=$\frac{7}{3-m}$,
∵关于x的方程$\frac{mx}{x-3}$-2=$\frac{1-x}{3-x}$的解为正数,
∴$\frac{7}{3-m}>0$,且$\frac{7}{3-m}≠3$
解得m<3,且m$≠\frac{2}{3}$.
点评 此题主要考查了分式方程的解,要熟练掌握,解答此类问题的关键是“转化思想”的应用,并要明确:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.


科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
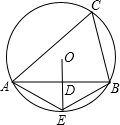 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com