
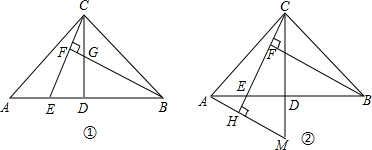
分析 (1)根据题意得到三角形ABC为等腰直角三角形,且CD为斜边上的中线,利用三线合一得到CD垂直于AB,且CD为角平分线,得到∠CAE=∠BCG=45°,再利用同角的余角相等得到一对角相等,AC=BC,利用ASA得到三角形AEC与三角形CGB全等,利用全等三角形的对应边相等即可得证;
(2)由等腰三角形的性质得出∠ACD=∠BCD=∠CBE=45°,利用AAS得到三角形BCE与三角形CAM全等,利用全等三角形的对应边相等即可得证.
解答 (1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
$\left\{\begin{array}{l}{∠CAE=∠BCG}&{\;}\\{AC=BC}&{\;}\\{∠ACE=∠CBG}&{\;}\end{array}\right.$,
∴△AEC≌△CGB(ASA),
∴AE=CG;
(2)解:CM=BE;理由如下:
∵AC=BC,∠ACB=90°,点D是AB的中点,
∴CD平分∠ACB,
∴∠ACD=∠BCD=∠CBE=45°,
∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
在△BCE和△CAM中,
$\left\{\begin{array}{l}{∠CMA=∠BEC}&{\;}\\{∠ACM=∠CBE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△BCE≌△CAM(AAS),
∴BE=CM.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等三角形是解本题的关键.


科目:初中数学 来源:2017届江苏省江阴市周庄学区九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
下列调查中,不适合采用抽样调查的是( )
A. 了解江阴市中小学生的睡眠时间 B. 了解无锡市初中生的兴趣爱好
C. 了解江苏省中学教师的健康状况 D. 了解“天宫二号”飞行器各零部件的质量
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3y+$\frac{1}{2}x$ | B. | $\frac{x+y}{3}-2y=0$ | C. | y=$\frac{2}{x}+1$ | D. | x2+y=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
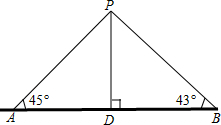 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 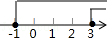 | B. | 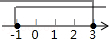 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com