练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知：直线y=kx+b平行于直线y=-3x+4且与y轴交于点（0，-5），则此函数的解析式为y=-3x-5．

    分析 先利用两直线平行得到k=-3，再把（0，-5）代入y=-3x+b中求出b即可．

    解答 解：∵直线y=kx+b平行于直线y=-3x+4，
    ∴k=-3，
    把（0，-5）代入y=-3x+b得b=-5，
    ∴此函数的解析式为y=-3x-5．
    故答案为y=-3x-5．

    点评 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；再将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；然后解方程或方程组，求出待定系数的值，进而写出函数解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
    若b′=$\left\{\begin{array}{l}{b，a≥1}\\{-b，a＜1}\end{array}\right.$，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5）．
    （1）①点（$\sqrt{3}$，1）的限变点的坐标是（$\sqrt{3}$，1）；
    ②在点A（-2，-1），B（-1，2）中有一个点是函数y=$\frac{2}{x}$图象上某一个点的限变点，这个点是（-1，2）；
    （2）若点P在函数y=-x+3（-2≤x≤k，k＞-2）的图象上，其限变点Q的纵坐标b′的取值范围是-5≤b′≤2，求k的取值范围5≤k≤8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若一次函数y=kx+b的图象经过点P（-2，3），则2k-b的值为（　　）
    A．2B．-2C．3D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如表：
    售价（元/件）100110120130…
    月销量（件）200180160140…
    已知该运动服的进价为每件60元，设售价为x元．销量该运动服每件的利润为y元，销量为W件，其中W与x成一次函数关系．
    （1）写出y与x的函数关系式；
    （2）求出W与x的函数关系式；
    （3）售价为150元时，月销售量是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

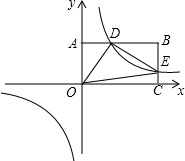    3．如图，反比例函数y=$\frac{k}{x}$（k＞0）与长方形OABC在第一象限相交于D、E两点，OA=2，OC=4，连结OD、OE、DE．记△OAD、△OCE的面积分别为S1、S2．
    （1）填空：①点B坐标为（4，2）；②S1=S2（填“＞”、“＜”、“=”）；
    （2）当S1+S2=2时，求：?k的值及点D、E的坐标；?试判断△ODE的形状，并求△ODE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

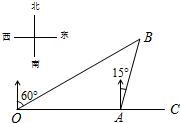    13．如图，港口A在观测站O的正东方向，OA=40海里，某船从港口A出发，沿北偏东15°方向航行半小时后到达B处，此时从观测站O处测得该船位于北偏东60°的方向．求该船航行的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．（1）计算：$\sqrt{2}$•sin45°+（3-π）0+（-2）
    （2）化简：（a-$\frac{a}{a+1}$）÷$\frac{1}{a+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知△ABC为边长为6的等边三角形，D、E分别在边BC、AC上，且CD=CE=x，连接
    DE并延长至点F，使EF=AE，连接AF、CF．
    （1）求证：△AEF为等边三角形；
    （2）求证：四边形ABDF是平行四边形；
    （3）记△CEF的面积为S，
    ①求S与x的函数关系式；
    ②当S有最大值时，判断CF与BC的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知抛物线y=a（x-3）2经过点A（2，$\frac{1}{2}$）．
    （1）写出抛物线的表达式，并指出抛物线的对称轴；
    （2）求出与点A（2，$\frac{1}{2}$）关于该抛物线的对称轴对称的点A′的坐标．

    查看答案和解析>>

    同步练习册答案