
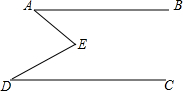
 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.分析 (1)过E作EF∥AB,根据平行线的性质,即可得出∠AEF=∠A,∠DEF=∠D,再根据∠AED=∠AEF+∠DEF=∠A+∠D进行计算即可;
(2)与(1)中方法一样,过E作EF∥AB,根据平行线的性质,即可得出∠AEF=∠A,∠DEF=∠D,再根据∠AED=∠AEF+∠DEF=∠A+∠D进行计算即可;
(3)过E作EF∥AB,根据平行线的性质,即可得出∠AEF=∠A,∠DEF=∠D,即可得到∠AED=∠AEF+∠DEF=∠A+∠D.
解答 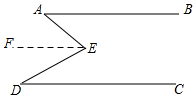 解:(1)如图,过E作EF∥AB,
解:(1)如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠AEF=∠A,∠DEF=∠D,
∴∠AED=∠AEF+∠DEF=∠A+∠D=30°+40°=70°.
故答案为:70°;
(2)如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠AEF=∠A,∠DEF=∠D,
∴∠AED=∠AEF+∠DEF=∠A+∠D=20°+60°=80°.
故答案为:80°;
(3)∠AED=∠EAB+∠EDC,
证明:如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠AEF=∠A,∠DEF=∠D,
∴∠AED=∠AEF+∠DEF=∠A+∠D.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线构造内错角,依据两直线平行,内错角相等进行判断.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.
如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
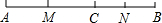 如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com