
【题目】某汽车专卖店计划购进甲、乙两种新型汽车共140辆,这两种汽车的进价、售价如下表:
进价(万元/辆) | 售价(万元/辆) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)若该汽车专卖店投入1000万元资金进货,则购进甲乙两种新型汽车各多少辆?
(2)若该汽车专卖店准备乙种型号汽车的进货量不超过甲种型号汽车的进货量的3倍,应怎样安排进货方案,才能使该汽车专卖店售完这两种新型汽车后获得的利润最大?最大利润是多少?(其它成本不计)
【答案】(1)65,75;(2)35,105
【解析】
试题分析:(1)设购进甲种新型汽车x辆,购进乙种新型汽车y辆,根据“购进甲、乙两种新型汽车共140辆、该汽车专卖店投入1000万元资金进货”列方程组求解;
(2)设购进a辆甲种新型汽车,则购进乙种新型车辆(140﹣a)辆,令该汽车专卖店售完这两种新型汽车后获得的利润为W,列出W关于a的函数关系式,由a的取值范围结合一次函数性质可得其最值情况.
试题解析:(1)设购进甲种新型汽车x辆,购进乙种新型汽车y辆,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:购进甲种新型汽车65辆,购进乙种新型汽车75辆;,
(2)设购进a辆甲种新型汽车,则购进乙种新型车辆(140﹣a)辆,
令该汽车专卖店售完这两种新型汽车后获得的利润为W,
根据题意,W=(8﹣5)a+(13﹣9)(140﹣a)=﹣a+560,
∵140﹣a≤3a,且a为整数,
∴a≥35,a为整数,
∵W随a的增大而减小,
∴当a=35时,W取得最大值,最大值为﹣35+560=525(万元),
即购进35辆甲种新型汽车,则购进乙种新型车辆105辆,
答:购进35辆甲种新型汽车,则购进乙种新型车辆105辆,获得的利润最大,最大利润是525万元.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD中,对角线AC,BD相交于点O,过点O作直线交AD于点E,交BC于点F,若□ABCD的面积为30cm2,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
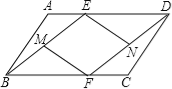
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 通过测试从9位书法兴趣小组的同学中,择优挑选5位去参加中学生书法表演,若测试结果每位同学的成绩各不相同.则被选中同学的成绩,肯定不少于这9位同学测试成绩统计量中的( )
A. 平均数B. 众数C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABOD的顶点A是函数y=-x-(k+1)的图象与函数y=![]() 在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C的坐标;
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com