练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

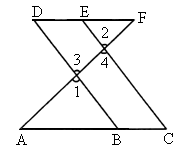
    填理由，已知如图，E为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证：DF∥AC．

    证明：∵∠1=∠2(已知)，∠1=∠3，∠2=∠4(　　)，∴∠3=∠4(等量代换)．

    ∴_____∥_______(　　)．

    ∴∠C=∠ABD(　　)

    ∵∠C=∠D(　　)，

    ∴∠D=∠ABD(　　)．

    ∴AC∥DF(　　)．

    答案：略
    解析：

    对顶角相等；BD,CE,内错角相等，两直线平行；两直线平行，同位角相等；已知；等量代换；内错角相等，两直线平行


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    12、已知如图直线l1∥l2，直线l3分别和l1、l2相交于A、B．求证∠1=∠3．（请在下列横线上填上合适的理由）．例：证明：因为l1∥l2
    已知
    ，所以∠1=∠2
    两直线平行，同位角相等
    ，又∠2=∠3
    对顶角相等
    ，所以∠1=∠3
    等量代换
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    填注理由：
    （1）已知如图1，∠1=∠2，∠3=∠4，求证：EG∥FH．
    证明：∵∠1=∠2（已知）∠AEF=∠1
    对顶角相等
    对顶角相等

    ∴∠AEF=∠2
    等量代换
    等量代换

    ∴AB∥CD
    同位角相等两直线平行
    同位角相等两直线平行

    ∴∠BEF=∠CFE
    两直线平行，内错角相等
    两直线平行，内错角相等

    ∵∠3=∠4（已知）
    ∴∠BEF-∠4=∠CFE-∠3
    等式的性质
    等式的性质

    即∠GEF=∠HFE
    ∴EG∥FH
    内错角相等两直线平行
    内错角相等两直线平行
    ．
    （2）如图2：已知，OC⊥OD，OA⊥OB，求证：∠1=∠3
    证明：∵OC⊥OD（已知）
    ∴∠1+∠2=90°
    垂直定义
    垂直定义

    同理∠3+∠2=90°
    ∴∠1=∠3
    等角的余角相等
    等角的余角相等
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    说理题：（将各步理由填在括号里）
    已知如图：EA⊥AD，FB⊥AD，∠E=∠F，问∠ECA=∠D吗？为什么？
    解：∠ECA=∠D，理由如下：
    因为EA⊥AD，FB⊥AD，
    所以EA∥FB（
    在同一平面内，垂直于同一直线的两条直线互相平行
    在同一平面内，垂直于同一直线的两条直线互相平行
     ）
    所以∠E=∠BHC（
    两直线平行，同位角相等
    两直线平行，同位角相等
     ）
    又因为∠E=∠F，
    所以∠F=∠BHC（
    等量代换
    等量代换
    ）
    所以EC∥FD（
    同位角相等，两直线平行
    同位角相等，两直线平行
     ）
    所以∠ECA=∠D（
    两直线平行，同位角相等
    两直线平行，同位角相等
     ）

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：068

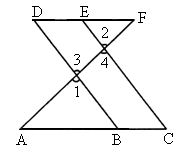
    填理由，已知如图，E为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证：DF∥AC．

    证明：∵∠1=∠2(已知)，∠1=∠3，∠2=∠4(　　)，∴∠3=∠4(等量代换)．

    ∴_____∥_______(　　)．

    ∴∠C=∠ABD(　　)

    ∵∠C=∠D(　　)，

    ∴∠D=∠ABD(　　)．

    ∴AC∥DF(　　)．

    查看答案和解析>>

    同步练习册答案